3. Интерполяция
3.1. Задача интерполяции
Пусть функция 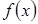 задана
набором точек задана
набором точек 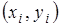 на
интервале на
интервале 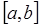 : :
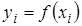 , , 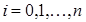 , , 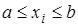 (3.1) (3.1)
Задача интерполяции – найти функцию 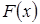 ,
принимающую в точках ,
принимающую в точках 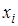 те
же значения те
же значения 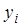 .
Тогда, условие интерполяции: .
Тогда, условие интерполяции:
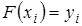 (3.2) (3.2)
При этом предполагается, что среди значений 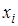 нет
одинаковых. Точки нет
одинаковых. Точки 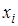 называют узлами интерполяции. называют узлами интерполяции.
Если 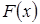 ищется только на отрезке ищется только на отрезке 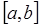 – то это задача интерполяции, а если за пределами первоначального отрезка, то это задача экстраполяции. – то это задача интерполяции, а если за пределами первоначального отрезка, то это задача экстраполяции.
Задача нахождения интерполяционной функции 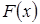 имеет много решений, так как через заданные точки имеет много решений, так как через заданные точки 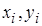 можно провести бесконечно много кривых, каждая
из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай интерполяции функции многочленами: можно провести бесконечно много кривых, каждая
из которых будет графиком функции, для которой выполнены все условия интерполяции. Для практики важен случай интерполяции функции многочленами:
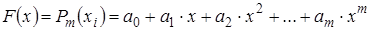 , , 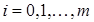 (3.3) (3.3)
При этом искомый полином называется интерполяционным полиномом.
При построении одного многочлена для всего рассматриваемого интервала 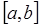 для нахождения коэффициентов многочлена необходимо решить систему уравнений, построенную на основе полинома (3.3). Данная система содержит для нахождения коэффициентов многочлена необходимо решить систему уравнений, построенную на основе полинома (3.3). Данная система содержит 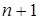 уравнение, следовательно, с ее помощью можно определить уравнение, следовательно, с ее помощью можно определить 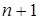 коэффициент. Поэтому максимальная степень интерполяционного многочлена коэффициент. Поэтому максимальная степень интерполяционного многочлена 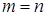 , и многочлен принимает вид , и многочлен принимает вид
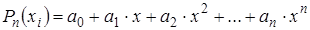 , , 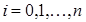 (3.4) (3.4)
3.2. Локальная и глобальная интерполяция
Если задан 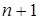 узел интерполяции, то на этих узлах можно построить один интерполяционный многочлен n-й степени, узел интерполяции, то на этих узлах можно построить один интерполяционный многочлен n-й степени, 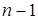 многочленов первой степени и большой набор многочленов степени меньше n, опирающиеся на некоторые из этих узлов. многочленов первой степени и большой набор многочленов степени меньше n, опирающиеся на некоторые из этих узлов.
Теоретически максимальную точность обеспечивает многочлен более высокой степени. Однако на практике наиболее часто используют многочлены невысоких степеней, во избежание погрешностей расчета коэффициентов при больших степенях многочлена.
Если функция 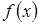 интерполируется на отрезке интерполируется на отрезке 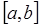 с помощью единого многочлена с помощью единого многочлена 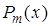 для всего отрезка, то такую интерполяцию называют глобальной. В случае локальной интерполяции на каждом интервале для всего отрезка, то такую интерполяцию называют глобальной. В случае локальной интерполяции на каждом интервале 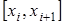 строится отдельный интерполяционный полином невысокой степени. строится отдельный интерполяционный полином невысокой степени.
3.3. Кусочно-линейная интерполяция
Простейшим и часто используемым видом локальной интерполяции является линейная (или кусочно-линейная) интерполяция. Она заключается в том, что узловые точки соединяются отрезками прямых (рис.3.1), то есть через каждые две точки 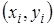 и и 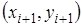 проводится прямая, то есть составляется полином первой степени: проводится прямая, то есть составляется полином первой степени:
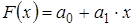 , при , при 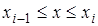 (3.5) (3.5)
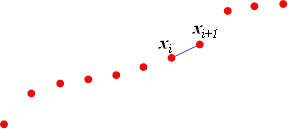
Рис. 3.1. Кусочно-линейная интерполяция
Коэффициенты 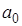 и и 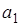 разные
на каждом интервале разные
на каждом интервале 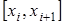 , и находятся из выполнения условий интерполяции на концах отрезка: , и находятся из выполнения условий интерполяции на концах отрезка:
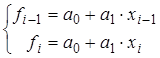 (3.6) (3.6)
Из системы уравнений (3.6) можно найти коэффициенты:
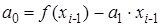 , , 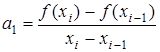 (3.7) (3.7)
При использовании кусочно-линейной интерполяции сначала нужно определить интервал, в который попадает значение x, а затем подставить его в выражение (3.5), используя коэффициенты для данного интервала.
3.4. Кусочно-квадратичная интерполяция
В случае квадратичной интерполяции, для каждых трех узловых точек 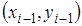 , , 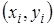 , , 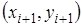 , строится уравнение параболы: , строится уравнение параболы:
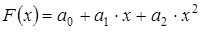 , при , при 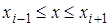 (3.8) (3.8)
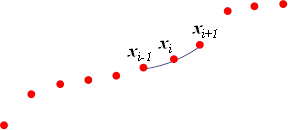
Рис.3.2. Кусочно-квадратичная интерполяция
Здесь коэффициенты 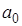 , , 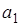 и и 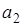 разные на каждом интервале разные на каждом интервале 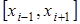 и определяются решением системы уравнений для условия прохождения параболы через три точки: и определяются решением системы уравнений для условия прохождения параболы через три точки:
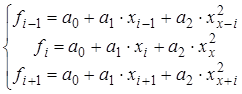 (3.9) (3.9)
Из системы уравнений (3.9) можно найти коэффициенты:
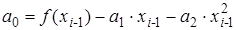
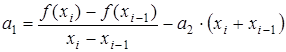 (3.10) (3.10)
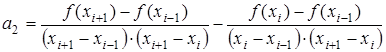
3.5. Многочлен Лагранжа
При глобальной интерполяции на всем интервале 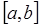 строится
единый многочлен. Одной из форм записи интерполяционного многочлена для глобальной интерполяции является многочлен Лагранжа: строится
единый многочлен. Одной из форм записи интерполяционного многочлена для глобальной интерполяции является многочлен Лагранжа:
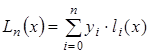 (3.11) (3.11)
где 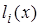 – базисные многочлены степени n: – базисные многочлены степени n:
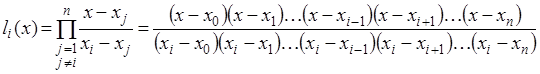 (3.12) (3.12)
То есть многочлен Лагранжа можно записать в виде:
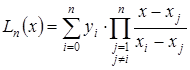 (3.13) (3.13)
Многочлен 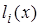 удовлетворяет условию удовлетворяет условию 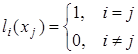 . Это условие означает, что многочлен равен нулю при каждом . Это условие означает, что многочлен равен нулю при каждом 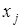 кроме кроме
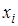 , то есть , то есть 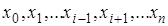 – корни этого многочлена. Таким образом, степень многочлена – корни этого многочлена. Таким образом, степень многочлена 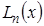 равна
n и при равна
n и при 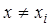 обращаются в ноль все слагаемые суммы, кроме слагаемого с номером обращаются в ноль все слагаемые суммы, кроме слагаемого с номером 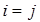 , равного , равного 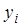 . .
Выражение (3.11) применимо как для равноотстоящих, так и для не равноотстоящих узлов. Погрешность интерполяции методом Лагранжа зависит от свойств функции 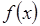 , от расположения узлов интерполяции и точки x. Полином Лагранжа имеет малую погрешность при небольших значениях n (n<20). При больших n погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (то есть его погрешность не убывает с ростом n). , от расположения узлов интерполяции и точки x. Полином Лагранжа имеет малую погрешность при небольших значениях n (n<20). При больших n погрешность начинает расти, что свидетельствует о том, что метод Лагранжа не сходится (то есть его погрешность не убывает с ростом n).
Многочлен Лагранжа в явном виде содержит значения функций в узлах интерполяции, поэтому он удобен, когда значения функций меняются, а узлы интерполяции неизменны. Число арифметических операции, необходимых для построения многочлена Лагранжа, пропорционально 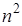 и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что с изменением числа узлов приходится все вычисления проводить заново. и является наименьшим для всех форм записи. К недостаткам этой формы записи можно отнести то, что с изменением числа узлов приходится все вычисления проводить заново.
Кусочно-линейная и кусочно-квадратичная локальные интерполяции являются частными случаями интерполяции многочленом Лагранжа.
3.6. Многочлен Ньютона
Другая форма записи интерполяционного многочлена – интерполяционный многочлен Ньютона с разделенными разностями.
Пусть функция 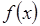 задана с произвольным шагом, и точки таблицы значений пронумерованы в произвольном
порядке. задана с произвольным шагом, и точки таблицы значений пронумерованы в произвольном
порядке.
Разделенные разности нулевого порядка совпадают со значениями функции в узлах. Разделенные разности первого порядка определяются через разделенные разности нулевого порядка:
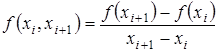 (3.14) (3.14)
Разделенные разности второго порядка определяются через разделенные разности первого порядка:
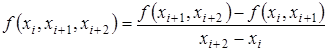 (3.15) (3.15)
Разделенные разности k-го порядка определяются через разделенные разности порядка 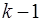 : :
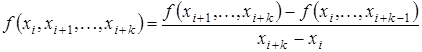 (3.16) (3.16)
Используя понятие разделенной разности интерполяционный многочлен Ньютона можно записать в следующем виде:
 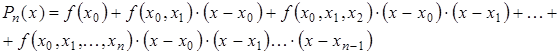 (3.17) (3.17)
За точностью расчета можно следить по убыванию членов суммы (3.17). Если функция достаточно гладкая, то справедливо приближенное равенство 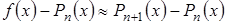 . Это приближенное равенство можно использовать для практической оценки погрешности
интерполяции: . Это приближенное равенство можно использовать для практической оценки погрешности
интерполяции: 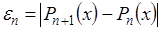 . .
|



