2.3. Метод Гаусса
В формулах численного интегрирования Ньютона-Котеса используются равноотстоящие узлы. В случае квадратурных формул
Гаусса узлы интегрирования 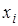 на
отрезке на
отрезке 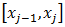 располагаются не равномерно, а выбираются таким образом, чтобы при наименьшем
возможном числе узлов точно интегрировать многочлены наивысшей возможной степени. располагаются не равномерно, а выбираются таким образом, чтобы при наименьшем
возможном числе узлов точно интегрировать многочлены наивысшей возможной степени.
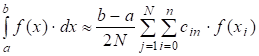 (2.17) (2.17)
Узлы 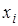 являются корнями полинома Лежандра степени n, а веса вычисляются интегрированием
полиномов Лежандра по формуле являются корнями полинома Лежандра степени n, а веса вычисляются интегрированием
полиномов Лежандра по формуле  , где , где 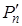 – первая производная полинома Лежандра. – первая производная полинома Лежандра.
Узлы и веса, рассчитанные для отрезка 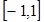 , приводятся в таблице 2.2. Для интегрирования на произвольном частичном отрезке необходимо пересчитать значения узлов для данного частичного отрезка , приводятся в таблице 2.2. Для интегрирования на произвольном частичном отрезке необходимо пересчитать значения узлов для данного частичного отрезка 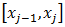 : :
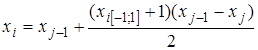 (2.18) (2.18)
Квадратура Гаусса относится к квадратурам открытого типа. Это означает, что ни один и узлов не совпадает ни с одним из концов отрезка интегрирования a или b.
Веса квадратур Гаусса всегда положительны, и при увеличении числа узлов точность приближения почти всегда возрастает.
| n |
i |
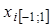 |
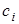 |
| 1 |
1 |
0 |
2 |
| 2 |
1 |
-0.5773503 |
1 |
| 2 |
0.5773503 |
1 |
| 3 |
1 |
-0.7745967 |
0.5555556 |
| 2 |
0 |
0.8888889 |
| 3 |
0.7745967 |
0.5555556 |
| 4 |
1 |
-0.8611363 |
0.3478548 |
| 2 |
-0.3399810 |
0.6521451 |
| 3 |
0.3399810 |
0.6521451 |
| 4 |
0.8611363 |
0.3478548 |
| 5 |
1 |
-0.9061798 |
0.4786287 |
| 2 |
-0.5384693 |
0.2369269 |
| 3 |
0 |
0.5688888 |
| 4 |
0.5384693 |
0.2369269 |
| 5 |
0.9061798 |
0.4786287 |
| 6 |
1 |
-0.9324700 |
0.1713245 |
| 2 |
-0.6612094 |
0.3607616 |
| 3 |
-0.2386142 |
0.4679140 |
| 4 |
0.2386142 |
0.4679140 |
| 5 |
0.6612094 |
0.3607616 |
| 6 |
0.9324700 |
0.1713245 |
Таблица 2.2. Весовые коэффициенты метода Гаусса
|



