2.2. Методы Ньютона-Котеса
2.2.1. Метод прямоугольников
Одним из простейших методов численного
интегрирования является метод прямоугольников. На частичном отрезке 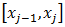 подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину
частичного отрезка подынтегральную функцию заменяют полиномом Лагранжа нулевого порядка, построенным в одной точке. В качестве этой точки можно выбрать середину
частичного отрезка 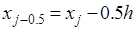 .
Тогда значение интеграла на частичном отрезке: .
Тогда значение интеграла на частичном отрезке:
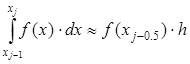 (2.6) (2.6)
Подставив это выражение в (2.4), получим составную формулу средних прямоугольников:
 (2.7) (2.7)
Графическая иллюстрация метода средних прямоугольников представлена на рис.2.2(a). Из рисунка видно, что площадь
криволинейной трапеции приближенно заменяется площадью многоугольника, составленного из N прямоугольников. Таким образом, вычисление
определенного интеграла сводится к нахождению суммы N элементарных прямоугольников.
Формулу (2.7) можно представить в ином виде:
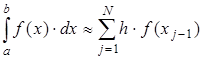 или или 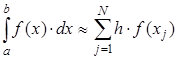 (2.8) (2.8)
Эти формулы называются формулой левых и правых прямоугольников соответственно. Графически метод левых и правых прямоугольников
представлен на рис.2.2(б, в). Однако из-за нарушения симметрии в формулах правых и левых прямоугольников, их погрешность значительно больше, чем в методе
средних прямоугольников.
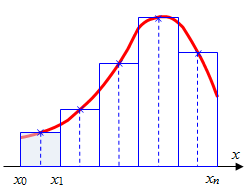
а) средние прямоугольники |
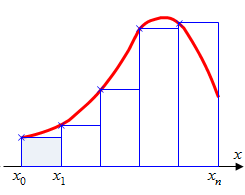
б) левые прямоугольники |
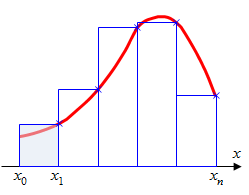
в) правые прямоугольники |
| Рис.2.2. Интегрирование методом прямоугольников |
2.2.2. Метод трапеций
Если на частичном отрезке 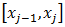 подынтегральную функцию заменить полиномом Лагранжа первой степени: подынтегральную функцию заменить полиномом Лагранжа первой степени:
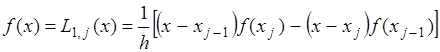 (2.9) (2.9)
то искомый интеграл на частичном отрезке запишется следующим образом:
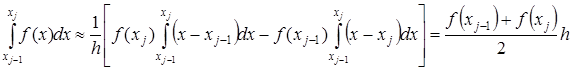 (2.10) (2.10)
Тогда составная формула трапеций на всем отрезке интегрирования 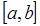 примет вид: примет вид:
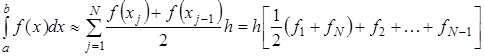 (2.11) (2.11)
Графически метод трапеций представлен на рис.2.3. Площадь криволинейной трапеции заменяется площадью многоугольника,
составленного из N трапеций, при этом кривая заменяется вписанной в нее ломаной. На каждом из частичных отрезков функция аппроксимируется прямой,
проходящей через конечные значения, при этом площадь трапеции на каждом отрезке определяется по формуле 2.10.
Погрешность метода трапеций выше, чем у метода средних прямоугольников. Однако на практике найти среднее значение на элементарном интервале можно только у функций, заданных аналитически (а не таблично), поэтому использовать метод средних прямоугольников удается далеко не всегда.
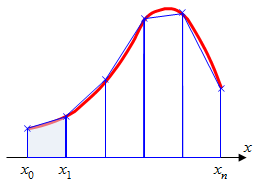
Рис.2.3. Интегрирование методом методом трапеций
2.2.3. Метод Симпсона
В этом методе подынтегральная функция на частичном отрезке 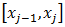 аппроксимируется параболой, проходящей через три точки аппроксимируется параболой, проходящей через три точки 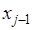 , , 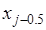 , , 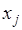 , то есть интерполяционным многочленом Лагранжа второй степени: , то есть интерполяционным многочленом Лагранжа второй степени:
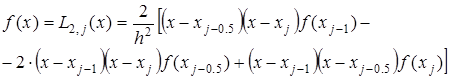 (2.12) (2.12)
Проведя интегрирование, получим:
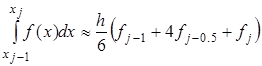 (2.13) (2.13)
Это и есть формула Симпсона или формула парабол. На
отрезке 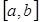 формула
Симпсона примет вид: формула
Симпсона примет вид:
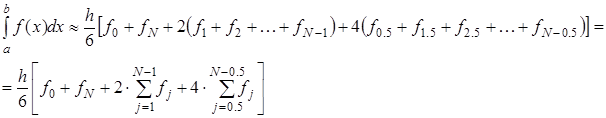 (2.14) (2.14)
Если разбить отрезок интегрирования 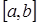 на четное количество 2N
равных частей с шагом на четное количество 2N
равных частей с шагом 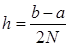 ,
то можно построить параболу на каждом сдвоенном частичном отрезке ,
то можно построить параболу на каждом сдвоенном частичном отрезке 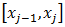 и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид: и переписать выражения (2.12-2.14) без дробных индексов. Тогда формула Симпсона примет вид:
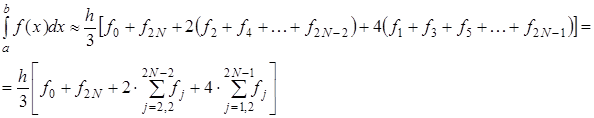 (2.15) (2.15)
Графическое представление метода Симпсона показано на рис.2.4. На каждом из сдвоенных частичных отрезков заменяем дугу данной кривой параболой.
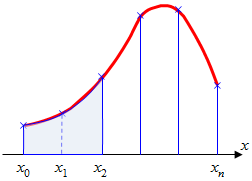
Рис.2.4. Метод Симпсона
2.2.4. Семейство методов Ньютона-Котеса
Выше были рассмотрены три схожих метода интегрирования функций – метод прямоугольников, метод трапеций, метод Симпсона.
Их объединяет общая идея: интегрируемая функция интерполируется на отрезке интегрирования по равноотстоящим узлам многочленом Лагранжа, для которого
аналитически вычисляется значение интеграла. Семейство методов, основанных на таком подходе, называется методами
Ньютона-Котеса.
В выражении 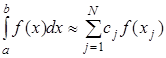 коэффициенты коэффициенты 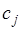 правильнее называть весовыми коэффициентами. Величину правильнее называть весовыми коэффициентами. Величину 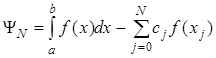 ,
определяющую погрешность численного интегрирования, называют остатком. ,
определяющую погрешность численного интегрирования, называют остатком.
Для семейства методов Ньютона-Котеса можно записать общее выражение:
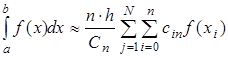 (2.16) (2.16)
где n – порядок метода Ньютона-Котеса, N – количество частичных отрезков, 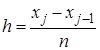 , , 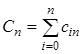 , , 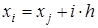 . .
Из выражения (2.16) легко можно получить формулу прямоугольников для 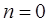 ,
формулу трапеций для ,
формулу трапеций для 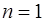 , и формулу Симпсона для , и формулу Симпсона для 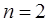 .
Коэффициенты .
Коэффициенты 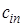 могут быть заданы в табличной форме (таблица.2.1). могут быть заданы в табличной форме (таблица.2.1).
| n |
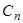 |
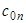 |
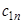 |
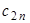 |
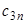 |
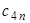 |
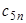 |
| 0 |
1 |
1 |
|
|
|
|
|
| 1 |
2 |
1 |
1 |
|
|
|
|
| 2 |
6 |
1 |
4 |
1 |
|
|
|
| 3 |
8 |
1 |
3 |
3 |
1 |
|
|
| 4 |
90 |
7 |
32 |
12 |
32 |
7 |
|
| 5 |
288 |
19 |
75 |
50 |
50 |
75 |
19 |
Таблица 2.1. Весовые коэффициенты метода Ньютона-Котеса
|



