1. Методы численного дифференцирования функций
Вычисление производной численными методами
имеет смысл либо, если аналитическое вычисление производной невозможно либо,
если аналитическое выражение неизвестно, и функция задана набором точек.
1.1. Методы односторонней разности
Производная функции 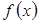 определяется выражением: определяется выражением:
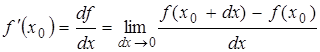 (1.1) (1.1)
Заменяя приращение dx на конечную
величину Δx, называемую шагом дифференцирования, получаем
выражение:
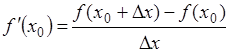 (1.2) (1.2)
Если дифференцируемая функция задана в виде
непрерывной функции (рис.1.1), то для вычисления значения дифференциала необходимо
получить значение функции 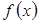 в
точке в
точке 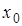 и в
точке и в
точке 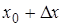 .
После чего можно вычислить значение производной функции .
После чего можно вычислить значение производной функции 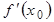 . .
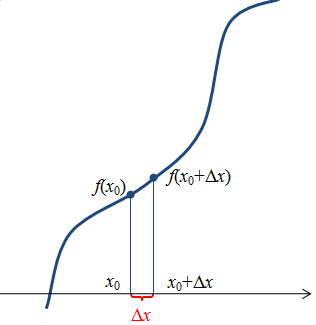
Рис.1.1.Непрерывная функция
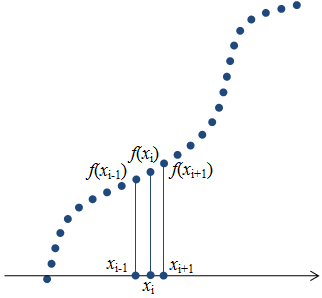
Если функция задана выборкой, то есть набором
значений функции в точках (рис.1.2), то выражение для численного
дифференцирования (при условии, что x образуют возрастающую
последовательность) можно переписать в виде:
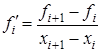 (1.3) (1.3)
 |
| f1 |
x1 |
| f2 |
x2 |
| … |
… |
| fi |
xi |
| … |
… |
| fn |
xn |
|
Рис.1.2. Дискретная функция
Как видно из этих выражений, значение
производной в точке 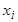 оценивается
по значению функции в этой и в следующей точке оценивается
по значению функции в этой и в следующей точке 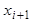 .
Такой способ можно условно назвать правосторонней разностью. Нетрудно
записать выражение для левосторонней разности: .
Такой способ можно условно назвать правосторонней разностью. Нетрудно
записать выражение для левосторонней разности:
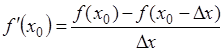 (1.4) (1.4)
или
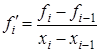 (1.5) (1.5)
1.2. Метод двусторонней разности
С точки зрения точности методы левосторонней и
правосторонней разностей равнозначны. Более точное значение дает метод двусторонней
разности (что особенно справедливо для гладких функций). Теорема Лагранжа
говорит о том, что уравнение:
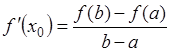 (1.6) (1.6)
(при условии, что 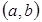 –
замкнутый промежуток, на котором функция –
замкнутый промежуток, на котором функция 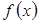 дифференцируема)
имеет по меньшей мере один корень дифференцируема)
имеет по меньшей мере один корень 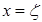 . Значение
этого корня, вообще говоря, зависит от вида функции . Значение
этого корня, вообще говоря, зависит от вида функции 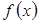 . Если
она квадратичная, то уравнение первой степени и его корень лежит в точности на
середине отрезка . Если
она квадратичная, то уравнение первой степени и его корень лежит в точности на
середине отрезка 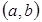 ,
то есть: ,
то есть:
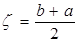 (1.7) (1.7)
Если a имеет постоянное значение, а b
стремится к a, то один из корней, как правило (за исключением случаев,
когда вторая производная 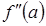 равна
нулю или не существует), стремится к середине отрезка, то есть равна
нулю или не существует), стремится к середине отрезка, то есть 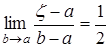 .
Поэтому более точное приближение к искомому значению производной функции в
точке .
Поэтому более точное приближение к искомому значению производной функции в
точке 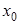 можно
получить, воспользовавшись формулами двусторонней разности: можно
получить, воспользовавшись формулами двусторонней разности:
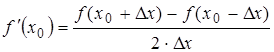 (1.8) (1.8)
или, для функций заданных в виде выборки:
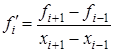 (1.9) (1.9)
Наглядно сравнить одностороннюю и двустороннюю
разности можно представив производную, как тангенс угла наклона касательной к
функции в точке xi. На рисунке 1.3 точное значение
производной обозначено как 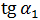 . В методе односторонней разности (рис.1.3, а) вместо касательной
проводится прямая через точки xi и xi+1.
Если в окрестностях точки xi функция не гладкая, то значение
производной ( . В методе односторонней разности (рис.1.3, а) вместо касательной
проводится прямая через точки xi и xi+1.
Если в окрестностях точки xi функция не гладкая, то значение
производной (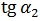 ) будет существенно отличаться от точного. В то время как в методе двусторонней
разности, проведя прямую через точки xi-1 и xi+1
(рис.1.3, б), можно получить значение производной практически совпадающее
с точным. ) будет существенно отличаться от точного. В то время как в методе двусторонней
разности, проведя прямую через точки xi-1 и xi+1
(рис.1.3, б), можно получить значение производной практически совпадающее
с точным.
|
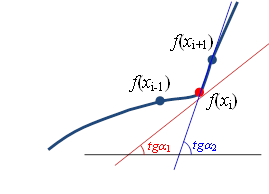
а) односторонняя разность
|
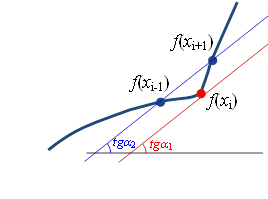
б) двусторонняя разность |
|
Рис.1.3. Графическое представление производной |
1.3. Частное дифференцирование функции многих переменных
Отдельно следует отметить случай численного
определения частных дифференциалов функций многих переменных. В этом случае все
аргументы функции становятся константами кроме аргумента, по которому
проводится дифференцирование, а требуемый порядок производной получается путем
последовательного вычисления производных, вплоть до требуемого порядка:
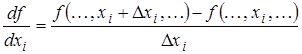 (1.10) (1.10)
1.4. Производные высоких порядков
При вычислении производных высоких порядков производная
(n)-го порядка считается первой производной от (n-1)-го порядка. Так вторая
производная функции является первой производной от первой производной:
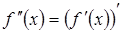 или или 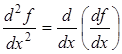 (1.11) (1.11)
Тогда выражение для вычисления производной
примет вид:
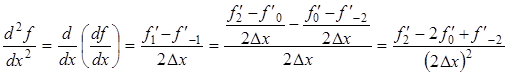 (1.12) (1.12)
|



