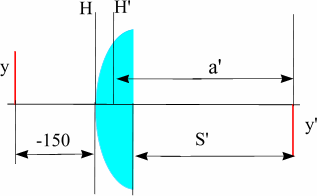
Предмет величиной 5 мм находится на расстоянии 150 мм перед выпуклоплоской
линзой с радиусом поверхности 50 мм, толщиной 10 мм и показателем преломления
1.5. Определить размер и положение изображения относительно последней
поверхности S'. Решить задачу с помощью матриц. Осуществить проверку решения.
Решение:
Сначала необходимо определить параксиальные характеристики системы.
По соотношениям, приведенным в практической работе 4, получим: f'=100;
SH=0 ; S'H=-6.67.
Составляем матрицу преобразования лучей системой, опорные плоскости
которой расположены в плоскостях предмета и изображения для данной задачи.
Очевидно, что преобразований будет три, от предмета до главной плоскости
- перенос T0, на главных плоскостях - преломление
R1, до изображения - перенос T1.
Итак, матрицы: 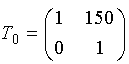
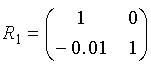
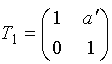
Матрица всей системы G=T1·R1·T0.
Правила перемножения матриц можно посмотреть в "Приложении
П3. Арифметические операции над матрицами". Результат произведения
матриц даст нам матрицу с одним неизвестным - a':
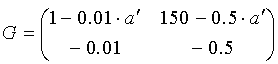
Условие сопряжения опорных плоскостей гласит, что элемент матрицы В=0.
Составляем уравнение 150-0.5a'=0, значит, a'=300.
S'=S'H+a'=300-6.67=293.33 мм.
Определение величины изображения. Изображение y'=y·β
Увеличение системы равно значению элемента А. β=1-3= -2.
y'= -2·5= -10.
Ответ: S'=293.33 мм, y'= -10 мм.
Проверка:
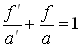
100/a'=1-(-100)/(-150)=1-2/3=1/3
a'=300, значит, S'=293.33 мм
Увеличение 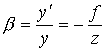 , значит,
β= -(-100)/(-50)= -2.
, значит,
β= -(-100)/(-50)= -2.
Ответ: S'=293.33 мм, y'= -10 мм.
Фокусное расстояние линзы f'=100 мм. Предмет находится на расстоянии
a= -150 мм от передней главной плоскости линзы. Изображение формируется
на расстоянии 300 мм от задней главной плоскости линзы. Найти значения
элементов матрицы преобразования лучей при условии, что опорные плоскости
совпадают с плоскостями предмета и изображения.
Решение:
Все элементы матрицы имеют свое назначение. Элементы A и D
зависят от линейного увеличения системы.
β= -f/z= -(-100)/(a-f)=100/(-150+100)=-2.
Тогда A=-2; D=1/А=-0.5.
Необходимо определить силу линзы Ф=1/f'=0.01, значит C=-0.01.
Элемент В для сопряженных плоскостей равен 0.
Ответ: Матрица преобразования
лучей данной системой: 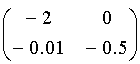 .
.



