Вернуться наверх
aco.ifmo.ru photonic
вернуться в оглавление предыдущая глава предыдущий параграф следующий параграф следующая глава

Практическое занятие №5.
Расчет характеристик системы с использованием матричной оптики

5.2. Расчет характеристик многокомпонентных оптических систем с использованием матриц

Вопросы расчета характеристик можно рассмотреть в основных определениях и соотношениях в параграфе "6.3. Матрицы оптической системы, состоящей из нескольких компонентов"

5.2.1. Пакет из плоскопараллельных слоев

Пакет плоскопараллельных слоев - это система, состоящая из сред с различными показателями преломления. Оптическая сила таких элементов равна нулю .

Приведенная матрица переноса для пакета плоскопараллельных слоев будет выглядеть следующим образом:

, где

Задача 1.

Пакет плоскопараллельных слоев состоит из трех пластин в воздухе, находящихся на расстоянии 11.00 и 5.00 мм соответственно. Толщины пластин d1=10.5 ; d2=9.00 и d3=3.4 мм.
Показатели преломления n1=2.1 ; n2=1.5 и n3=1.7. Найти матрицу преобразования лучей данной системы.

Решение:

Матрица пакета слоев будет иметь вид:

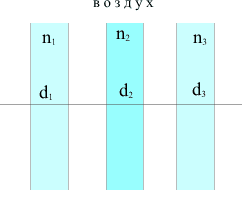Необходимо определить приведенные толщины слоев t: t1=10.5/2.1=5; t2=9/1.5=6; t3=2. И общая толщина всего пакта слоев равна сумме приведенных толщин и воздушных промежутков: t=5+11+6+5+2=29 мм.

Ответ: Матрица преобразования пакета:

Причем, вопрос в задачах может касаться не только всей матрицы, но и отдельных ее элементов. Как видите, сложный расчет в данной матрице касается только одного элемента B, тогда как остальные требуют не расчета, а простого знания структуры матрицы.

5.2.2. Оптическая система с нулевыми расстояниями между компонентами

Рассмотрим оптическую систему, в которой расстояния между компонентами равны нулю . Матрица такой системы:

  

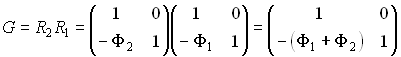
то есть оптические силы таких компонент складываются:

Задача 2.

Компонент из трех тонких линз (с нулевыми расстояниями между ними) находится в воздухе. Определить значение элемента C матрицы преобразования лучей. Известно, что фокусные расстояния имеют следующие значения: f'1=10, f'2=-20 и f'3=5 мм.

Решение

Общая оптическая сила этой системы будет равна сумме отдельных оптических сил. Необходимо определить приведенные силы линз Ф:
Ф1=0.1, Ф2=-0.05 и Ф3=0.2.

Общая суммарная сила системы Ф=0.3-0.05=0.25 [1/мм=кдптр].

Элемент матрицы С=-Ф=-0.25

Ответ: Элемент матрицы С=-0.25

В задачах может быть предложен поиск и других элементов матрицы, но расчета требует только элемент С, а остальные нам известны заранее. Также задачи могут касаться поиска фокусного расстояния одного из элементов по заданной общей оптической силе.