Практическое занятие №2.
Правило знаков в оптике. Основные законы распространения света
2.3. Задачи на закон отражения
Закон отражения состоит в том, что угол падения равен углу отражения.
Подробно тема изложена в параграфе "3.1.2.
Закон отражения". Рассмотрим примеры, имеющие практическое значение:
2.3.1. Нахождение изображения в плоском зеркале
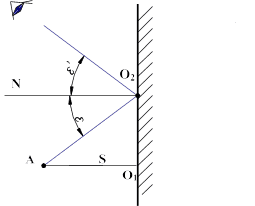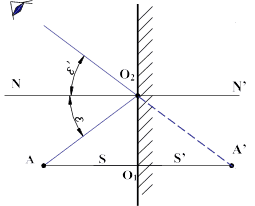
2.3.2. Поворот плоского зеркала
Зависимость между углом поворота зеркала и поворотом выходящего луча
представляет большой интерес.
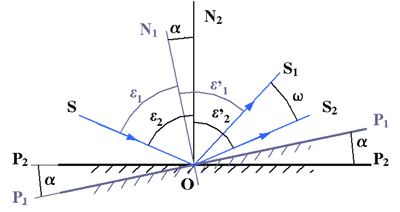
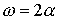
Значит при повороте плоского зеркала на угол 30°, отраженный луч повернется
на 60°.
Задача 1.
Определить угол поворота плоского зеркала γ относительно оси ОХ,
если направление падающего луча задано углом α=10°, а направление
отраженного луча β=80°.
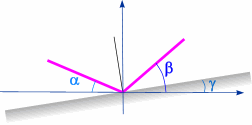
Решение:
Угол падения равен углу отражения. Если угол отражения не равен углу
падения, значит, зеркало повернуто. Разница между углами составляет
70°. Как известно, угол поворота луча в два раза больше угла поворота
зеркала.
В нашем случае угол поворота луча составляет 70 °. Это означает,
что γ=35°.
Ответ: γ=35°
2.3.3. Два плоских зеркала, расположенных под углом
Угловое зеркало - часто используемая в оптике конструкция.
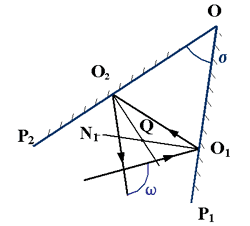
Зависимость между направлениями падающего и выходящего лучей для системы,
состоящей из двух зеркал : 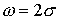 . .
1. Угол отклонения равен удвоенной величине угла между зеркалами.
2. При повороте двойного зеркала угол отклонения не изменяется
3. Угол отклонения не зависит от угла падения
Задача 2.
Угловое зеркало изменяет направление падающего на него луча на величину
γ=30°. Определить угол при вершине зеркала.
Решение:
Угловое зеркало поворачивает луч на угол, равный удвоенному углу при
вершине зеркала.
Значит, угол при вершине равен 15°.
Ответ: Угол при вершине двойного
зеркала равен 15°.
|



