Практическое занятие №2.
Правило знаков в оптике. Основные законы распространения света
2.2. Задачи на закон преломления
Закон преломления установлен
голландским математиком и астрономом Снеллиусом в 1626 (XVII век), а французский
ученый Декарт в 1637 привел этот закон к более удобной математической
форме. Подробно закон преломления рассмотрен в параграфе "3.1.1.
Закон преломления"
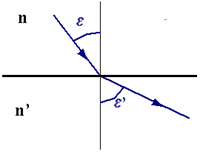
Падающий луч, преломленный луч и нормаль в точке падения луча лежат в
одной плоскости.
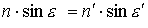
Произведение показателя преломления на синус угла, образованного лучом
с нормалью в точке падения, остается постоянным при переходе через преломляющую
поверхность.
Задача
Объект находящийся в воде, виден под углом 60°.
Определить угол наклона преломленного луча в воде, если показатель преломления
n=1.33.
Решение:
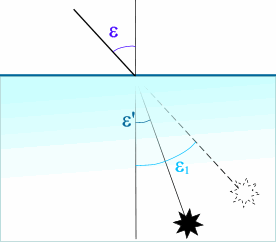
Угол, под которым виден объект - это угол мнимый, а реально это угол,
под которым мы смотрим на объект. Таким образом, нам даны ε1
и n.
По закону преломления n·sin ε=n'·sin ε'
sin(ε')=sin(ε)/n'
sin(ε')=sin(60°)/1.33=0.709
Преломленный угол ε' равен 40°30'
Ответ: Угол ε'=40°30'
|



