6.3. Матрицы оптической системы, состоящей из нескольких компонентов

Любую оптическую систему можно представить как совокупность нескольких компонентов, разделенных промежутками. Пусть дана некоторая произвольная система, в которой для каждого компонента известно положение главных плоскостей и оптическая сила, а также известны расстояния между компонентами и показатели преломления (на рис.6.3.1 указаны расстояния непосредственно между главными плоскостями компонентов).

Рис.6.3.1. Оптическая система из нескольких компонентов.

Матрица такой системы будет состоять из произведения матриц преломления и переноса для отдельных компонентов:

      (6.3.1)

где , .

Каждый из компонентов может быть разложен по этой же схеме на более простые составляющие (вплоть до отдельных поверхностей).

Если между компонентами нет промежутков (), то матрица переноса между этими компонентами становится единичной , и ее можно не учитывать. Если оптическая сила компонента равна нулю , то матрица преломления для этого компонента также становится единичной .

6.3.1. Пакет из плоскопараллельных слоев

Рассмотрим оптическую систему, состоящую из компонентов, оптическая сила которых равна нулю (рис.6.3.2).

Рис.6.3.2. Пакет из плоскопараллельных слоев.

Матрица такой системы состоит только из матриц переноса:

      (6.3.2)

Приведенные толщины всех элементов складываются, и могут заменены общей приведенной толщиной:

      (6.3.3)

Действие на проходящие лучи пакета слоев с разными геометрическими толщинами и показателями преломления эквивалентно одному слою, толщина которого равна приведенной толщине.

Таким образом, приведенная матрица переноса для пакета из плоскопараллельных слоев будет выглядеть следующим образом:

(6.3.4)

6.3.2. Оптическая система с нулевыми расстояниями между компонентами

Рассмотрим оптическую систему, в которой расстояния между компонентами равны нулю . Матрица такой системы:

      (6.3.5)

то есть оптические силы таких компонент складываются:

(6.3.6)

6.3.3. Двухкомпонентная оптическая система

Рассмотрим оптическую систему, состоящую из двух компонентов, разделенных ненулевым промежутком.

Матрица такой системы:

      (6.3.7)

Оптическая сила:

      (6.3.8)

Рассмотрим частные случаи двухкомпонентной системы.

• Если , тогда .
• Если , это значит, что второй компонент (его главная плоскость) находится в заднем фокусе первого компонента. Тогда , то есть второй компонент может иметь какую угодно оптическую силу.
• Если , то первый компонент находится в переднем фокусе второго компонента, тогда .
• Если , тогда .

Афокальные (телескопические) системы

Афокальные или телескопические системы – это системы из двух или более компонентов, оптическая сила которых равна нулю. Такие системы предназначены для наблюдения удаленных объектов.

У афокальных систем оптическая сила равна нулю, то есть , следовательно, определитель матрицы . Отсюда . Тогда матрица будет выглядеть следующим образом:

      (6.3.9)

Если опорные плоскости сопряжены, то , и следовательно:

(6.3.10)

Тогда координаты луча:

      (6.3.11)

Из выражения (6.3.11) видно, что для афокальной системы элемент матрицы равен линейному (поперечному) увеличению, а его обратная величина имеет смысл углового увеличения:

      (6.3.12)

      (6.3.13)

В телескопических системах линейное и угловое увеличение не зависят от положения сопряженных опорных плоскостей и, следовательно, не зависят от положения предмета и изображения:

      (6.3.14)

Двухкомпонентная оптическая система телескопическая, если задний фокус первого компонента совпадает с передним фокусом второго (рис.6.3.3):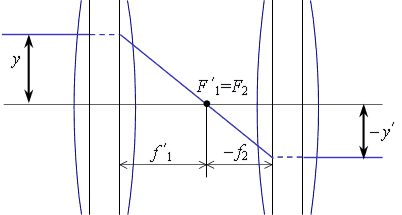

      (6.3.15)

Рис.6.3.3. Положение фокусов компонентов телескопической системы.

Линейное увеличение такой системы:

      (6.3.16)

Матрица тонкой линзы

Рассмотрим линзу в воздухе. Такую линзу можно рассматривать как двухкомпонентную систему, состоящую из двух поверхностей, разделенных промежутком (рис.6.3.4).

Рис.6.3.4. Линза в воздухе.

Для линзы в воздухе , следовательно . Тогда матрица преобразования линзы в общем случае будет выглядеть следующим образом:

      (6.3.17)

Элементы полученной матрицы преобразования можно выразить через параксиальные характеристики, как показано в выражении (6.2.10). Таким образом, зная матрицу преобразования линзы, можно найти ее параксиальные характеристики.

У тонкой линзы толщина по оси равна нулю . У такой линзы матрица преобразования:

(6.3.18)

где – оптическая сила тонкой линзы, , – кривизны поверхностей.

6.3.4. Расчет параксиальных (нулевых) лучей через оптическую систему

Нулевые лучи – это лучи, которые преломляются по законам параксиальной оптики, но имеют произвольно большие координаты.

Расчет нулевых лучей через оптическую систему состоит из операций переноса луча между компонентами и преломления луча на компонентах, которые можно описывать либо в матричной форме (6.2.3), (6.3.1), либо в виде рекуррентных соотношений:

      (6.3.19)

Например, – перенос до первого компонента, – преломление после первого компонента.

Вычисления согласно выражениям (6.3.19) выполняются столько раз, сколько компонентов имеется в оптической системе. Однако, для полного расчета лучей через оптическую систему вначале нужно определить координаты лучей в пространстве предметов, а после завершения расчетов определить координаты лучей в пространстве изображений. Таким образом, расчет нулевых (параксиальных) лучей включает в себя три этапа:

• определение входных координат луча,
• вычисление хода луча (последовательное определение его координат на всех компонентах),
• определение выходных координат луча.

Решение задач на расчет характеристик оптической системы с использованием матриц преобразования рассматривается в практическом занятии "Расчет характеристик системы с использованием матричной оптики".

Вычисление параксиальных характеристик оптической системы с использованием матричной оптики рассматривается в приложении "Вычисление и отображение параксиальных характеристик при помощи матричной оптики".