

|
|
|||||


|
|||||
|
| |||||
4.1. Приближение коротких длин волн. Уравнение эйконалаГеометрическая оптика – это раздел оптики, в котором
считается, что длина волны пренебрежимо мала Вначале рассмотрим известные из математики тождества,
справедливые для некоторой функции Таким образом: Пусть теперь Тогда, применив преобразование (4.1.3), получим следующее
выражение: В итоге получим следующее уравнение: Поскольку в левой части уравнения (4.1.8) – комплексное
число, то равенство нулю правой части предполагает равенство нулю как
вещественной, так и мнимой частей этого комплексного числа. Нас интересует
вещественная часть: Перепишем это уравнение в виде: где Применим к уравнению (4.1.10) приближение
коротких длин волн. Если длина волны стремится к нулю
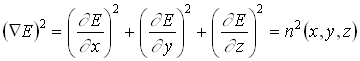 (4.1.12) (4.1.12)
Из уравнения эйконала следует, что геометрическая оптика применима только для коротких длин волн. Чем короче длина волны, тем точнее приближение геометрической оптики. |