Вернуться наверх

Лабораторная работа №6.
Моделирование прохождения света через оптические детали

6.3. Пример выполнения работы

6.3.1. Задание (построение хода лучей через призму Дове (АР-0))

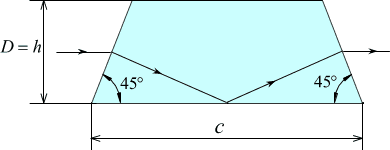Призма АР-0

Отражательные призмы используют для изменения направления оси оптической системы и оборачивания изображения в заданном направлении. Призма АР-0 - равнобедренная призма с одной отражающей гранью. Выходящий из призмы луч отклоняется на 0° относительно падающего. Исходной величиной для расчета параметров призмы является диаметр входного пучка :
,

Задача заключается в том, чтобы вычислить и отобразить ход любого луча через призму АР-0.

Этапы выполнения задания
1. Анализ программы-заготовки (`pr_ar0.pas` или `prizm_ar0.zip`).

Перед выполнением задания необходимо проанализировать работу программы-заготовки, которая содержит подпрограммы отображения призмы АР-0 и произвольного луча.
При рисовании начало координат находится в точке начала луча.

2. Проектирование структуры данных и организации вычислений.

Необходимо организовать вычисление углов преломления и отражения произвольного луча на гранях призмы и отобразить ход луча.

Входными данными являются:

показатель преломления призмы
диаметр входного пучка
угол между лучом и осью

Краткий перечень необходимых действий для расчёта и отображения хода произвольного луча через призму АР-0 имеется в программе-заготовке.

3. Тестирование программы.

Необходимо протестировать программу с различными входными данными.

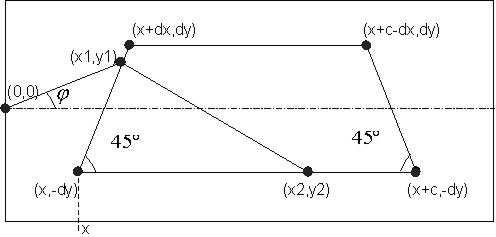
6.3.2. Система координат и координаты точек призмы

В первую очередь необходимо определить систему координат на рисунке, а затем координаты всех вершин призмы в этой системе координат. Начало координат по оси X находится в крайней левой точке окна рисунка, а по оси Y - в середине окна. Для определения координат всех граней призмы можно использовать несколько параметров: x - координата крайней левой точки призмы, с - длина грани призмы и h - высота призмы.

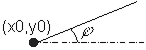
Параметры dx и dy вычисляются исходя из конфигурации призмы, в данном случае они будут вычисляться следующим образом:

Луч выходит из точки начала координат . Точку пересечения луча и первой грани призмы обозначим (x1, y1).

6.3.3. Уравнения прямой

Для нахождения точки пересечения луча и грани призмы можно воспользоваться уравнениями прямой. Уравнения прямой могут составлены исходя из разных начальных данных:

Уравнения прямой через две точки		Уравнения прямой через точку и направление

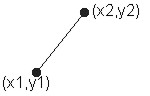
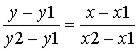
6.3.4. Координаты точки пересечения грани и луча в общем виде

Уравнение грани удобнее всего составить как уравнение прямой через две точки, а уравнение луча - как уравнение прямой через точку и направление. Точку пересечения грани и луча можно найти из системы уравнений грани и луча. Если решить эти уравнения в общем виде, то результат будет следующим:

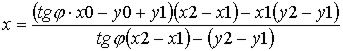
6.3.5. Координаты точки пересечения первой грани и луча

Теперь надо подставить координаты точек первой грани и первого луча в выражение для точки пересечения в общем виде:

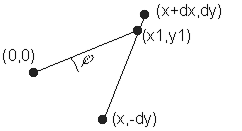
(x1, y1) заменяем на (x, -dy)
(x2, y2) заменяем на (x+dx, dy)
(x0, y0) заменяем на (0, 0) (x, y) заменяем на (x1, y1)

В итоге получается выражение для вычисления координат точки пересечения первой грани и луча:

6.3.6. Углы падения и преломления

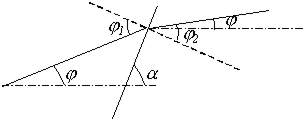
Чтобы вычислить угол, под которым идет луч после первой грани, необходимо:

перевести угол луча относительно оси () в угол луча относительно нормали к грани ():
вычислить угол преломления (), то есть угол преломленного луча относительно нормали:
перевести угол преломленного луча относительно нормали () в угол преломленного луча относительно оси ():

6.3.7. Программная реализация отображения первого отрезка луча

Рассмотрим теперь как записать нахождение точки встречи первого луча с первой гранью в тексте программы:

...
!    описание дополнительных переменных
       var dx, dy, x0,y0,x1, y1, alfa,fi,fi_pr,PI : real;      

...

{------ необходимо добавить следующие действия: ----------------}
      PI:=3.14159;
      alfa:=PI/4.;
      dy:=prizm_h/2;
      dx:=prizm_h/tan(alfa);
{ первый отрезок луча}
{   вычисление точки (x1,y1) встречи луча с первой гранью}
      x1:=(-dy*dx-2*x*dy)/(tan(ray_fi)*dx-2*dy);
      y1:=tan(ray_fi)*x1;
{   рисование луча от предмета до первой грани}
      x0:=0;
      y0:=0;
      Draw_Ray(x0,y0,ray_fi,x1);
{   вычисление угла падения луча на первую грань (fi)}
      fi:=PI/2+ray_fi-alfa;
{   вычисление угла преломления луча на первой грани (fi_pr)}
      fi_pr:=asin(sin(fi)/prizm_n);
{   вычисление угла между лучом и осью (ray_fi)}
      ray_fi:=alfa+fi_pr-PI/2;

...

Все переменные, участвующие в вычислениях, необходимо определить как real.

Нахождение точки встречи с остальными гранями делается аналогично.

Лабораторная работа №6. Моделирование прохождения света через оптические детали