Приложение А. Параксиальные характеристики оптической системы
В геометрической оптике для удобства чтения оптических схем и компьютерных расчетов приняты единые правила знаков (рис. А.1):
- положительным направлением света считается его распространение слева направо;
- осевые расстояния между преломляющими поверхностями считаются положительными, если они измеряются по направлению распространения света , то есть слева направо;
- радиус кривизны поверхности считается положительным, если центр кривизны находится справа от поверхности (поверхность обращена выпуклостью влево);
- угол между лучом и оптической осью считается положительным, если для совмещения оси с лучом ось нужно вращать по часовой стрелке;
- отрезки, перпендикулярные оптической оси, считаются положительными, если они располагаются над осью.
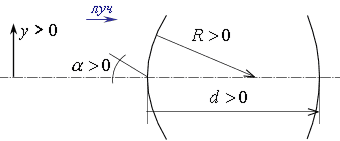
Рис. А.1. Правило знаков.
Одним из основных понятий геометрической оптики являются сопряженные точки – точки, одна из которых является изображением другой в соответствии с законами оптики.
Еще одним важным понятием геометрической оптики являются кардинальные точки и отрезки оптической системы. Их называют также параксиальными характеристиками, так как они строго
выполняются только в параксиальной области (бесконечно близко к оптической оси), в которой отсутствуют аберрации.
Главными плоскостями системы называется пара сопряженных плоскостей, в которых линейное увеличение равно единице. Главные точки  и и 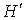 – это точки пересечения главных плоскостей с оптической осью. – это точки пересечения главных плоскостей с оптической осью.
Плоскость, сопряженная с бесконечно удаленной плоскостью предметов, называется задней фокальной плоскостью, а точка пересечения этой плоскости с оптической осью – задним
фокусом  (рис. А.2). Расстояние от задней главной точки до заднего фокуса называется задним фокусным расстоянием (рис. А.2). Расстояние от задней главной точки до заднего фокуса называется задним фокусным расстоянием  . Если . Если 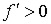 , то система называется собирающей (положительной). Если , то система называется собирающей (положительной). Если  , то система рассеивающая (отрицательная). Расстояние от последней поверхности до заднего фокуса называется задним фокальным отрезком , то система рассеивающая (отрицательная). Расстояние от последней поверхности до заднего фокуса называется задним фокальным отрезком
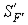 . .
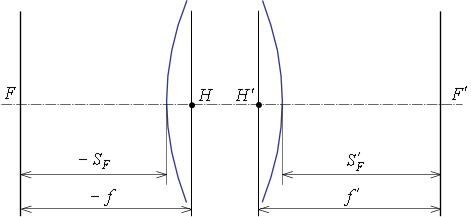
Рис. А.2. Кардинальные точки и отрезки.
Передний фокус 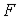 – это точка на оптической оси в пространстве предметов, сопряженная с бесконечно удаленной точкой, расположенной на оптической оси в
пространстве изображений. Если лучи выходят из переднего фокуса, то они идут в пространстве изображений параллельно. Переднее фокусное расстояние – это точка на оптической оси в пространстве предметов, сопряженная с бесконечно удаленной точкой, расположенной на оптической оси в
пространстве изображений. Если лучи выходят из переднего фокуса, то они идут в пространстве изображений параллельно. Переднее фокусное расстояние  – это расстояние от передней главной точки до переднего фокуса. Передний фокальный отрезок – это расстояние от передней главной точки до переднего фокуса. Передний фокальный отрезок  – это расстояние от первой поверхности до переднего фокуса. – это расстояние от первой поверхности до переднего фокуса.
Переднее и заднее фокусные расстояния не являются абсолютно независимыми, они связаны между собой соотношением:
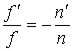 или или  , , |
(А.1) |
где 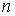 – показатель преломления в пространстве предметов, а – показатель преломления в пространстве предметов, а  – показатель преломления в пространстве изображений. – показатель преломления в пространстве изображений.
В том случае, если оптическая система находится в однородной среде (например, в воздухе), то  , следовательно, переднее и заднее фокусные расстояния равны по абсолютной величине , следовательно, переднее и заднее фокусные расстояния равны по абсолютной величине  . .
|



