Нелинейная фильтрация
Все линейные алгоритмы фильтрации приводят к сглаживанию резких перепадов яркости изображений, прошедших обработку. Линейные процедуры являются оптимальными при гауссовском распределении сигналов, помех и наблюдаемых данных. Обычно этому условию отвечают шумовые помехи на изображениях, поэтому при их подавлении линейные алгоритмы имеют высокие показатели. А если, например, задача обработки изображения состоит в выявлении границ объекта, то линейная фильтрация не подходит для ее решения.
Реальные изображения не подчиняются данному распределению вероятностей (разнообразные перепады яркости на границах, переходы от одной текстуры к другой и т. п.). Приходится иметь дело с изображениями, искаженными помехами других типов. Одной из них является импульсная помеха. При ее воздействии на изображении наблюдаются белые или (и) черные точки, хаотически разбросанные по кадру. Применение линейной фильтрации в этом случае неэффективно - каждый из входных импульсов ( по сути - дельта-функция) дает отклик в виде импульсной характеристики фильтра, а их совокупность способствует распространению помехи на всю площадь кадра.
Удачным решением перечисленных проблем является применение медианной фильтрации. Отметим, что медианная фильтрация представляет собой эвристический метод обработки, ее алгоритм не является математическим решением строго сформулированной задачи. Также как и в методе масочной фильтрации, при применении медианного фильтра происходит последовательная обработка каждой точки кадра, а для вычисления оценки используется некоторая окрестность (окно). Наиболее часто применяются варианты окон в виде креста и в виде квадрата. Размеры окна изменяются в зависимости от задаче и характера изображения. Отсчеты изображения, оказавшиеся в пределах окна, образуют рабочую выборку текущего шага.
Обозначим рабочую выборку в виде одномерного массива 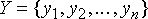 ; число его элементов равняется размеру окна, а их расположение произвольно. Обычно применяют окна с нечетным числом точек n (это автоматически обеспечивается при центральной симметрии апертуры и при вхождении самой центральной точки в ее состав). Если упорядочить последовательность ; число его элементов равняется размеру окна, а их расположение произвольно. Обычно применяют окна с нечетным числом точек n (это автоматически обеспечивается при центральной симметрии апертуры и при вхождении самой центральной точки в ее состав). Если упорядочить последовательность 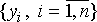 по возрастанию, то ее медианой (средним значением) будет тот элемент выборки, который занимает центральное положение в этой упорядоченной последовательности. Полученное таким образом число и является продуктом фильтрации для текущей точки кадра. Понятно, что результат такой обработки в самом деле не зависит от того, в какой последовательности представлены элементы изображения в рабочей выборке. Формальное обозначение описанной процедуры выглядит следующим образом: по возрастанию, то ее медианой (средним значением) будет тот элемент выборки, который занимает центральное положение в этой упорядоченной последовательности. Полученное таким образом число и является продуктом фильтрации для текущей точки кадра. Понятно, что результат такой обработки в самом деле не зависит от того, в какой последовательности представлены элементы изображения в рабочей выборке. Формальное обозначение описанной процедуры выглядит следующим образом:
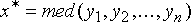
Предположим, что апертура фильтра находится вблизи границы, разделяющей светлый и темный участки изображения, при этом ее центр располагается в области темного участка. Тогда, вероятнее всего, рабочая выборка будет содержать большее количество элементов с малыми значениями яркости, и, следовательно, медиана будет находиться среди тех элементов рабочей выборки, которые соответствуют этой области изображения. Ситуация меняется на противоположную, если центр апертуры смещен в область более высокой яркости.
Рассмотрим пример. Предположим, что выборка имеет вид: {136, 110, 99, 45, 250, 55, 158, 104, 75}, а элемент 250, расположенный в ее центре, соответствует текущей точке фильтрации 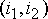 . Упорядоченная по возрастанию выборка имеет при этом вид: {45, 55, 75, 99, 104, 110, 136, 158, 250}, следовательно, получаем . Упорядоченная по возрастанию выборка имеет при этом вид: {45, 55, 75, 99, 104, 110, 136, 158, 250}, следовательно, получаем 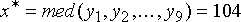 . Как видим, влияние соседей на результат фильтрации в текущей точке привело к игнорированию импульсного выброса яркости, что следует рассматривать как эффект фильтрации. Если импульсная помеха не является точечной, а покрывает некоторую локальную область, то она также может быть подавлена. Это произойдет, если размер этой локальной области будет меньше, чем половина размера окна. Поэтому для подавления импульсных помех, поражающих локальные участки изображения, следует увеличивать размеры окна. . Как видим, влияние соседей на результат фильтрации в текущей точке привело к игнорированию импульсного выброса яркости, что следует рассматривать как эффект фильтрации. Если импульсная помеха не является точечной, а покрывает некоторую локальную область, то она также может быть подавлена. Это произойдет, если размер этой локальной области будет меньше, чем половина размера окна. Поэтому для подавления импульсных помех, поражающих локальные участки изображения, следует увеличивать размеры окна.
Аналогично, строятся фильтры максимумов и минимумов.
Для выполнения медианной фильтрации библиотека IPL предоставляет функцию iplMedianFilter, которая имеет следующий прототип:
void iplMedianFilter(IplImage* srcImage, IplImage* dstImage, int nCols, int nRows, int anchorX, int anchorY);
где srcImage – указатель на исходное изображение, а dstImage – указатель на изображение, в котором будет сохраняться результат, nCols – размер окна по горизонтали, nRows – размер окна по вертикали, anchorX и anchorY – координата рабочей точки в системе координат окна.
Для выполнения нелинейной фильтрации максимумов и минимумов библиотека IPL предоставляет функции, которые имеют следующие прототипы:
void iplMaxFilter(IplImage* srcImage, IplImage* dstImage, int nCols, int nRows, int anchorX, int anchorY);
void iplMinFilter(IplImage* srcImage, IplImage* dstImage, int nCols, int nRows, int anchorX, int anchorY);
где srcImage – указатель на исходное изображение, а dstImage – указатель на изображение, в котором будет сохраняться результат, nCols – размер окна по горизонтали, nRows – размер окна по вертикали, anchorX и anchorY – координата рабочей точки в системе координат окна.
void NonlinearFilter(IplImage* img, int filter)
{
// Скопировать исходное изображение во временное
IplImage* tmp = iplCloneImage (img);
switch(filter)
{
case -1:
{
// Выполнить нелинейную фильтрацию минимумов
iplMinFilter(m_img, tmp, 3, 3, 1, 1);
break;
}
case 0:
{
// Выполнить нелинейную медианную фильтрацию
iplMedianFilter(m_img, tmp, 3, 3, 1, 1);
break;
}
case 1:
{
// Выполнить нелинейную фильтрацию максимумов
iplMaxFilter(m_img, tmp, 3, 3, 1, 1);
break;
}
}
// Освободить память исходного изображения
iplDeallocate(img, IPL_IMAGE_ALL );
// Скопировать результат в исходное изображение
img=iplCloneImage(tmp);
// Освободить память временного изображения
iplDeallocate(tmp, IPL_IMAGE_ALL );
}
Для медианной фильтрации цветных изображений в библиотеке IPL предусмотрена специальная функция:
void iplColorMedianFilter(IplImage* srcImage, IplImage* dstImage, int nCols, int nRows, int anchorX, int anchorY);
где srcImagedstImage – указатель на изображение, в котором будет сохраняться результат, nColsnRowsanchorX и anchorY
Функция iplMedianFilter обрабатывет цветовые плоскости изображения отдельно, вследствие чего цветовая корреляция изображения до и после фильтрации отсутствует. Функция iplColorMedianFilter вычисляет медиану используя следующее значение (цветовое расстояние): abs(R(i) - R(j)) + abs(G(i) - G(j)) + abs(B(i) - B(j)), где
|



