

|
|
|||||


|
|||||
|
| |||||
Приложение П2.
|
Для того чтобы найти параксиальные характеристики системы, необходимо вычислить ее матрицу преобразования, которая определяется как последовательное перемножение матриц преломления и переноса всех элементов оптической системы.
Матрица преломления оптической поверхности выглядит следующим образом:
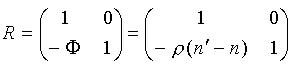 ,
где
,
где ![]() -
кривизна поверхности,
-
кривизна поверхности, ![]()
![]() ,
- показатели преломления до и после поверхности.
,
- показатели преломления до и после поверхности.
Матрица переноса от одной поверхности до другой выглядит следующим образом: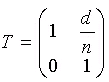 ,
где
,
где ![]() -
приведенное расстояние между оптическими поверхностями.
-
приведенное расстояние между оптическими поверхностями.
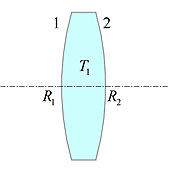 |
Матрицы преломления для данной оптической системы будут выглядеть следующим образом:
Матрица переноса между поверхностями будет такая:
|
Матрица преобразования оптической системы, состоящей из нескольких компонентов,
разделенных промежутками, будет состоять из произведения матриц преломления
![]() и матриц переноса
и матриц переноса ![]() для
отдельных компонентов:
для
отдельных компонентов:
![]()
Матрица преобразования для данной оптической системы:
![]()
Элементы матрицы преобразования можно выразить через кардинальные отрезки
оптической системы:
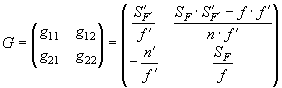 ,
,
где ![]() -
показатель преломления после оптической системы (в нашем случае
-
показатель преломления после оптической системы (в нашем случае ![]() ).
).
Зная значение элементов матрицы преобразования оптической системы, можно
определить значения параксиальных характеристик:
![]()
![]()
![]()
![]()
![]()
![]()
В соответствии с правилом знаков, все положительные отрезки откладываются слева направо, а отрицательные - справа налево.
Отложим (в соответствии с правилом знаков) передний и задний вершинные отрезки и найдем главные плоскости.
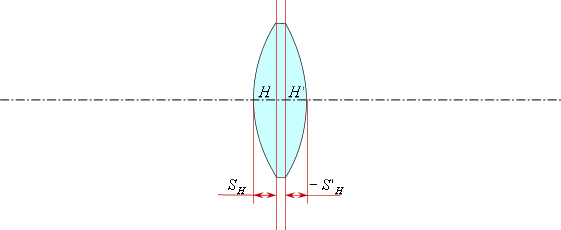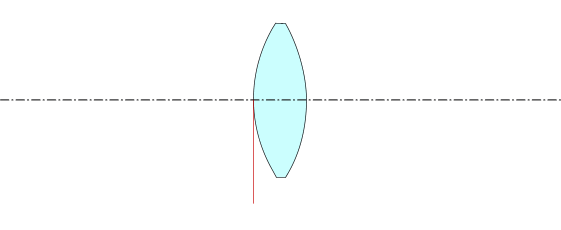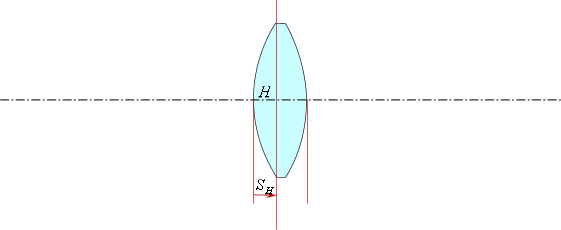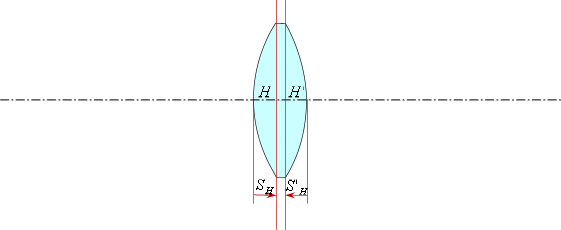
Передний вершинный отрезок ![]() - это расстояние от первой поверхности до передней главной плоскости.
- это расстояние от первой поверхности до передней главной плоскости.
Задний вершинный отрезок ![]() - это расстояние от последней поверхности до задней главной плоскости.
- это расстояние от последней поверхности до задней главной плоскости.
В данном случае передний вершинный отрезок ![]() -
положительный, следовательно, откладываем от первой поверхности вправо.
Задний вершинный отрезок
-
положительный, следовательно, откладываем от первой поверхности вправо.
Задний вершинный отрезок ![]() -
отрицательный, следовательно, откладываем его от последней поверхности
влево.
-
отрицательный, следовательно, откладываем его от последней поверхности
влево.
Теперь отложим передний и задний фокальные отрезки и найдем положение фокусов.
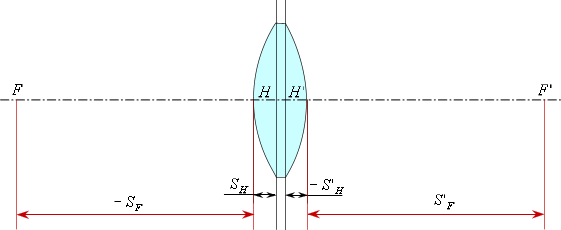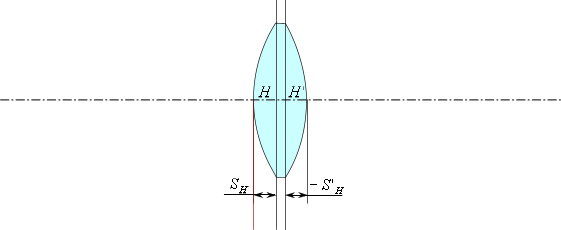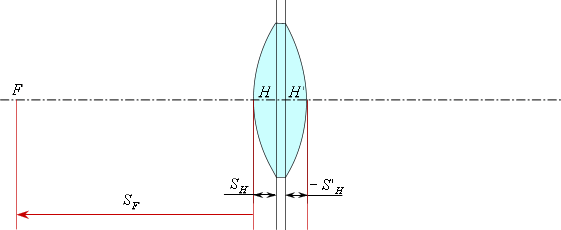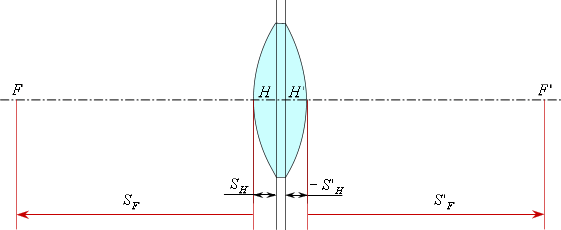
Передний фокальный отрезок ![]() -
это расстояние от первой поверхности до переднего
фокуса.
-
это расстояние от первой поверхности до переднего
фокуса.
Задний фокальный отрезок ![]() - это расстояние от последней поверхности до заднего
фокуса.
- это расстояние от последней поверхности до заднего
фокуса.
В данном случае передний фокальный отрезок ![]() - отрицательный, следовательно, откладываем его от первой поверхности
влево. Задний фокальный отрезок
- отрицательный, следовательно, откладываем его от первой поверхности
влево. Задний фокальный отрезок ![]() - положительный, следовательно, откладываем его от последней поверхности
вправо.
- положительный, следовательно, откладываем его от последней поверхности
вправо.
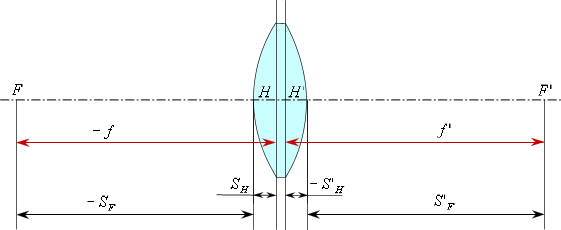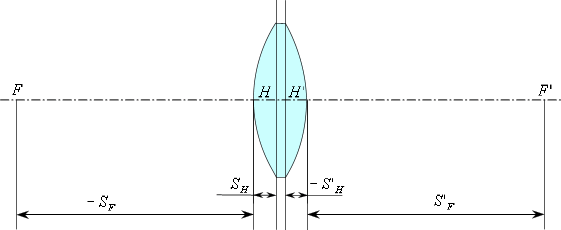
Переднее фокусное расстояние ![]() - это расстояние от передней главной
точки до переднего фокуса.
- это расстояние от передней главной
точки до переднего фокуса.
Заднее фокусное расстояние ![]() -
это расстояние от задней главной точки до заднего фокуса.
-
это расстояние от задней главной точки до заднего фокуса.
В данном случае переднее фокусное расстояние ![]() - отрицательное, следовательно, откладываем его от передней главной точки
влево. Заднее фокусное расстояние
- отрицательное, следовательно, откладываем его от передней главной точки
влево. Заднее фокусное расстояние ![]() - положительное, следовательно, откладываем его от задней главной точки
вправо.
- положительное, следовательно, откладываем его от задней главной точки
вправо.