Практическое занятие №5.
Расчет характеристик системы с использованием матричной оптики

5.4. Расчет параксиальных характеристик линзы с использованием матриц

Матрица тонкой линзы

Линзы и диоптрические (преломляющие) элементы можно рассматривать как многокомпонентные системы, состоящие из поверхностей, разделенных промежутками. Например, линзу в воздухе можно представить в матричном виде:

Задача

Перед стеклянным стержнем с выпуклой поверхностью радиусом 20 мм на расстоянии 100 мм расположен предмет. Величина предмета y=10 мм. Определить величину и положение изображения внутри стеклянного стержня, если показатель преломления среды стержня n=1.5.

Решение:

Сначала необходимо определить этапы построения изображения этой системой.

Этапа получается три: перенос от предмета до преломляющей поверхности - T₀, преломление - R, перенос до изображения - T₁.

Определим матрицы:

;

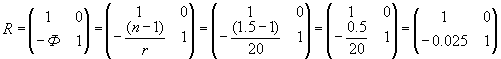
Произведение матриц даст нам матрицу G преобразования лучей этой системой.

Положение изображения:

Для сопряжения ОП и ОП' условие B=0.

100-x=0. Значит, х=100 - изображение находится на расстоянии 100 мм от края стержня.

Размер изображения:

Величина A - линейное увеличение, а величина D - обратная ей.

Значит, β=1/-1.5=-0.66. Величина изображения y'= β·y=-0.66·10=-6.6 мм. Изображение будет перевернутым.

Ответ: Перевернутое изображение величиной 6.6 мм будет находиться внутри стержня на расстоянии 100 мм от края.

Пример определения параксиальных характеристик системы по матрице Гаусса изложен в "Приложении П2. Вычисление и отображение параксиальных характеристик при помощи матричной оптики".