Вернуться наверх
aco.ifmo.ru photonic
вернуться в оглавление предыдущая глава предыдущий параграф следующий параграф следующая глава

Практическое занятие №4.
Определение параксиальных параметров линз различных типов

4.2. Определение параксиальных параметров линз с одной плоской поверхностью

Плоско-выпуклая линза

Параксиальные характеристики:



Для линз, у которых одна поверхность плоская, определено одно свойство, вытекающее из соотношений для параксиальных характеристик: через вершину неплоской поверхности проходит главная плоскость.

Другая главная плоскость находится на расстоянии d/n от плоской поверхности.

Соотношения для остальных линз этого типа определить несложно, поэтому можете это сделать самостоятельно.

 

Выпукло-плоская

Плоско-вогнутая

Вогнуто-плоская

Задача 1.

Предмет величиной 5 мм находится на расстоянии 150 мм перед выпуклоплоской линзой с радиусом поверхности 50 мм, толщиной 10 мм и показателем преломления 1.5. Определить размер и положение изображения относительно последней поверхности S'.

Решение:

Сначала необходимо определить параксиальные характеристики системы. В соответствии с выше рассмотренными соотношениями, имеем: f'=100; SH=0; S'H=-6.67.

Это означает, что в нашем примере a=s=-150.

Положение изображения

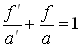
100/a'=1-(-100)/(-150)=1-2/3=1/3.

a'=300, значит, S'=SH'+a'=293.33 мм

Величина изображения

β=-f/z, где z=S-Sf=s-f=150-(-100)=-50 мм.

β= -(-100)/(-50)= -2.

y'=β·y= -10 мм.

Ответ: S'=293.33 мм, y'= -10 мм.

Также пример расчета положения/увеличения предмета/изображения можно увидеть в примере выполнения "Лабораторной работы №2. Определение параксиальных параметров склеенного объектива".

Задача 2.

Найти показатель преломления плосковогнутой линзы, если оптическая сила Ф=-12.50 дптр. Радиус поверхности по абсолютной величине составляет 40 мм.

Решение:

От показателя преломления зависит оптическая сила линзы:

Преобразуем: (1-n)=Ф·r2;

Показатель преломления: n=1-Ф·r2=1-(-0.0125·40)=1+0.5=1.5

Ответ: n=1.5