Вернуться наверх
aco.ifmo.ru photonic
вернуться в оглавление предыдущая глава предыдущий параграф следующий параграф следующая глава

Практическое занятие №3.
Построение хода лучей в оптической системе

3.4. Примеры решения задач

3.4.1. Построение сложного изображения

Решение задач на построение сложного изображения сводится к более простой задаче и решается традиционным способом. Предмет, состоящий из нескольких точек строится как результат построения данных точек на предмете.

Задача 1.

Построить изображение предмета. Положительная линза.

Решение:

    1. Сначала строим изображение нижней точки предмета розовыми лучами.
    2. Затем - изображения второй точки синими лучами.
    3. Соединяя эти точки, получаем изображение предмета.

Задача 2.

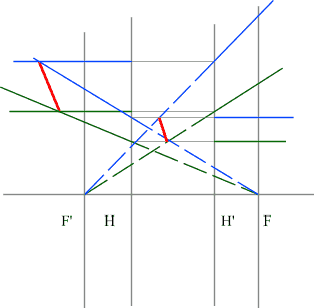
Построить изображение предмета. Положительная линза.

Решение:

  1. Сначала строим изображение верхней точки предмета синими лучами. Как и положено для рассеивающей линзы, пересекаться будут не сами лучи, а их продолжения.
  2. Затем строим изображение второй точки зелеными лучами.
  3. Соединяя эти точки, получаем изображение предмета.

    

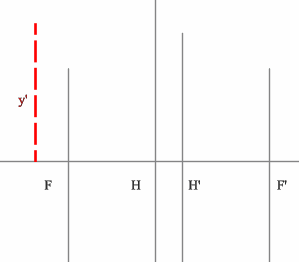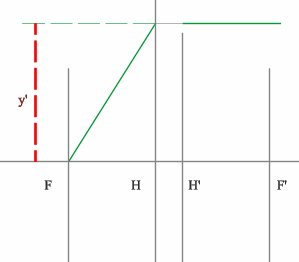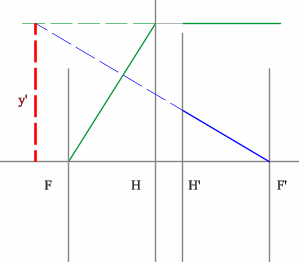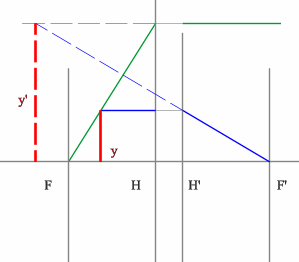
3.4.2. Построение предмета по заданному изображению

Построение предмета по изображению сводится к решению обратной задачи. Суть та же, что и в построении изображения.

Необходимы 2 луча, идущие через точку изображения. Пересечение этих лучей в пространстве предметов, даст нам точку предмета.

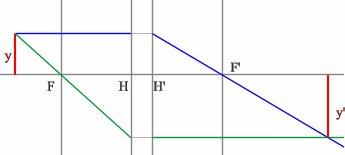
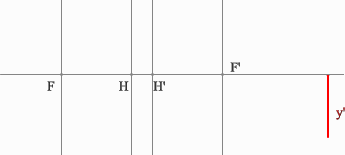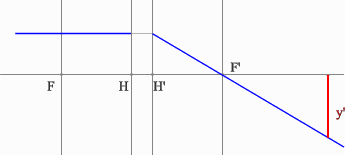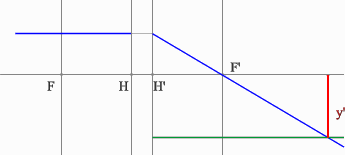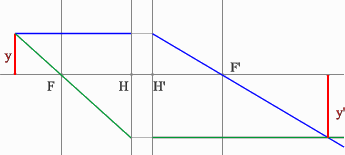
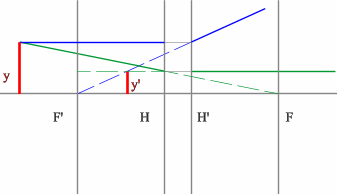
  1. Проводим луч через край изображения параллельно оптической оси. Преломленный луч пройдет через точку переднего фокуса.
  2. Проведем луч через край изображения и точку заднего фокуса. В пространстве предметов луч пойдет параллельно оптической оси.
  3. На пересечении построенных лучей находится искомое изображение точки предмета.

Положительная линза (построение предмета для действительного изображения)

   

Положительная линза (построение предмета для мнимого изображения)

   

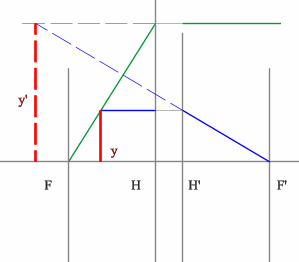
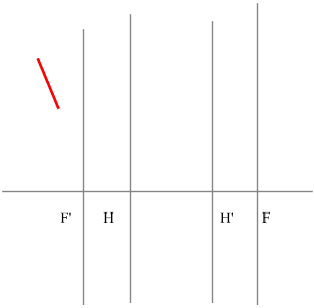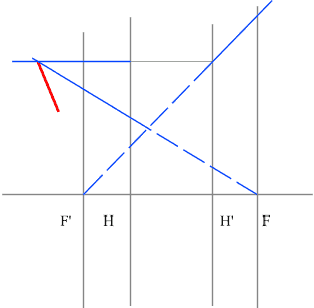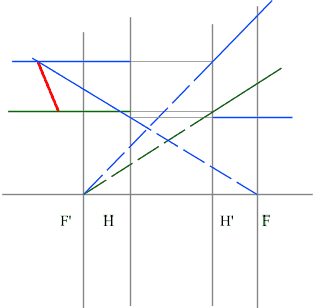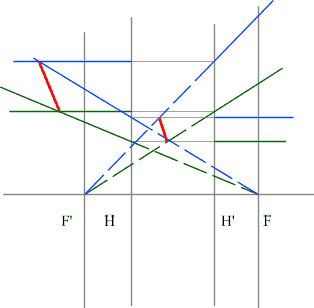
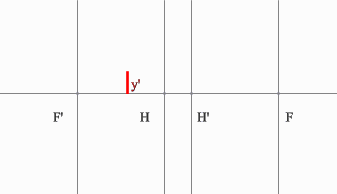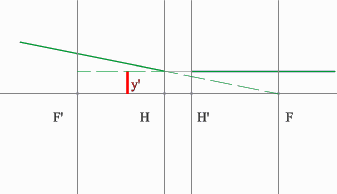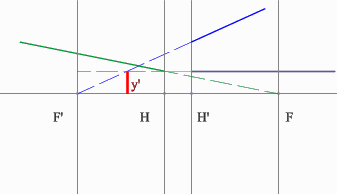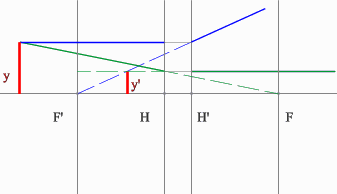
Отрицательная линза

   

3.4.3. Определение положения кардинальных точек и плоскостей системы

Решение задач этого типа основано на том, что среда однородная. Поэтому правомерно проводить луч через центр линзы. Этот луч пойдет после системы под тем же углом, что и до системы. Угловое увеличение равно единице.

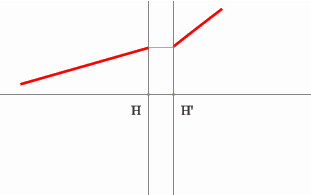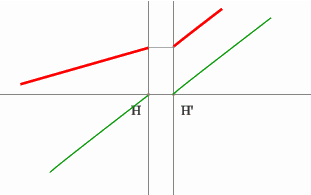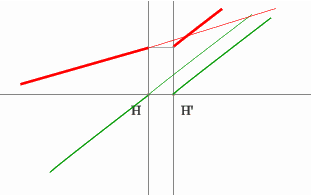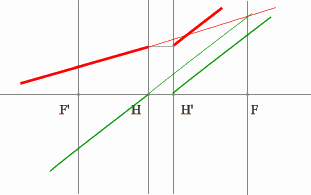
Задача 3.

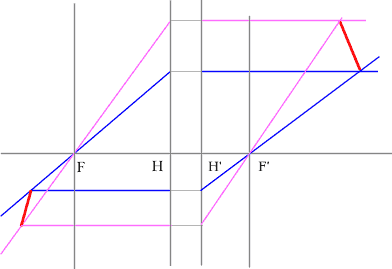
Определить положение фокальных плоскостей по заданному ходу луча. Система находится в однородной среде.

Решение:

Для построения необходимо воспользоваться уже знакомым правилом: лучи, идущие параллельно друг другу, сойдутся в одной точке на задней фокальной плоскости.

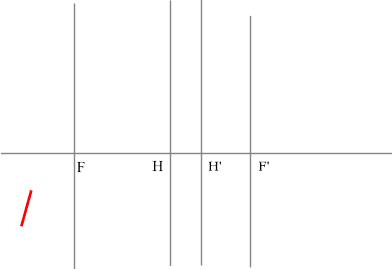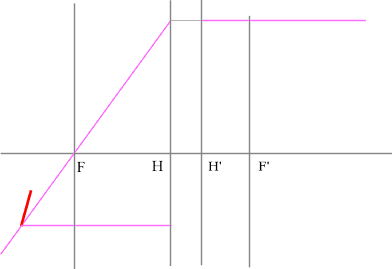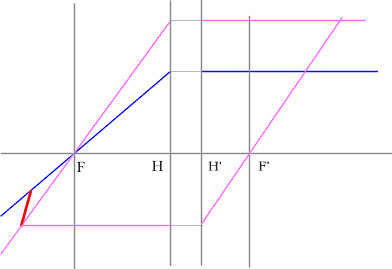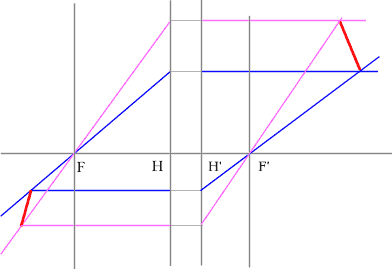
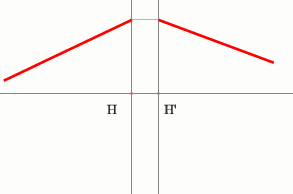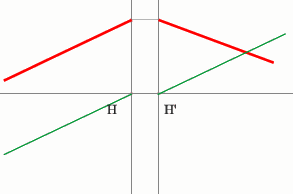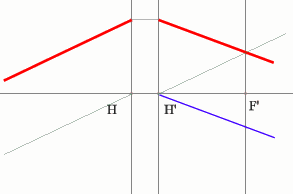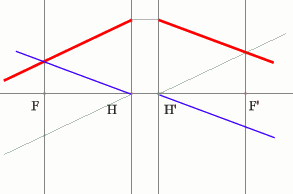
Последовательность построения:

  1. Строим луч параллельный заданному лучу через центр линзы. В пространстве изображений этот луч идет под тем же углом.
  2. Находим точку пересечения заданного и построенного лучей в пространстве изображений.
  3. По правилу, точка пересечения находится на задней фокальной плоскости системы.
  4. Если среда однородная, то построение передней фокальной плоскости можно не производить, отложив полученное расстояние от передней главной плоскости.

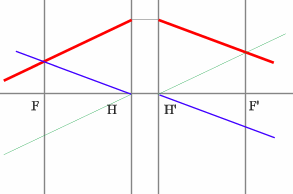
    Но на рисунке показано получение и передней и задней фокальных плоскостей с помощью построения:

Задача 4.

Определить положение фокальных плоскостей по заданному ходу луча. Система находится в однородной среде.

Решение:

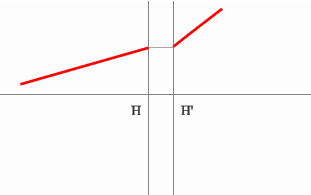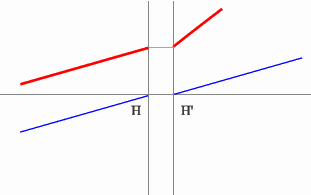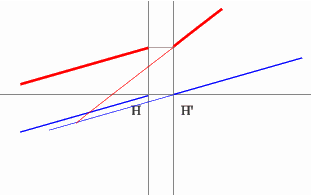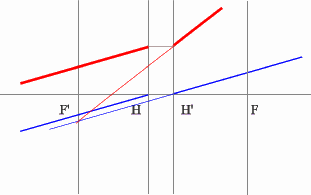
Строим синий луч, параллельный заданному в пространстве предметов.

Находим точку пересечения этого луча с заданным в пространстве изображений. Как видно из рисунка, пересекутся лишь продолжения лучей, что говорит о рассеивающем характере системы.

Через точку пересечения проходит задняя фокальная плоскость.

   

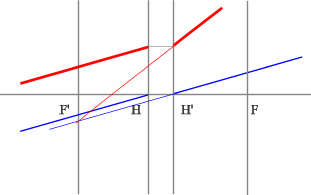
Поиск передней фокальной плоскости основан на том же принципе:

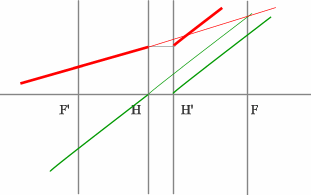
В пространстве изображений строим через центр линзы зеленый луч, параллельный заданному. В постранстве предметов этот луч пойдет под тем же углом и пересечет заданный луч в плоскости переднего фокуса системы. Найдя пересечение лучей, находим передний фокус.