Лабораторная работа №4.
Исследование аберраций осевой точки

4.3. Указания по выполнению работы.

Задание:

4.3.1. Создание оптической системы

Прежде всего, необходимо создать оптическую систему с заданными параметрами в программе для расчета оптических систем (например, OPAL-PC ). Подробное описание работы с OPAL-PC приведено в приложении «Описание работы с программой OPAL-PC». Создать новую оптическую систему можно при помощи пункта «Файл / Новая оптическая система». Предмет находится в бесконечности (дальнего типа), изображение - ближнего типа. Поскольку в данной работе рассматриваются аберрации осевого пучка, величину предмета можно задать равной нулю. Диафрагму можно поставить на первой поверхности. Длины волн: , , .

Переднюю апертуру можно сосчитать, зная относительное отверстие, но для этого нужно знать фокусное расстояние, поэтому вначале можно задать произвольную величину передней апертуры (например, 1 мм), а после выполнения вычислений заменить ее правильным значением.

После задания конструктивных параметров (пункт «Система / Конструктивные параметры») можно посмотреть значение параксиальных характеристик (пункт «Система / Параксиальные характеристики») и вычислить диаметр входного зрачка:

Теперь в OPAL-е можно задать правильную переднюю апертуру:

4.3.2. Определение аберраций осевого пучка

Аберрации осевого пучка можно посмотреть в пункте «Анализ Габаритов и аберраций / Аберрации осевого пучка». В текстовом режиме можно посмотреть числовые значения аберраций, а графическом - графики аберраций (переключение режимов по клавише «F6» ).

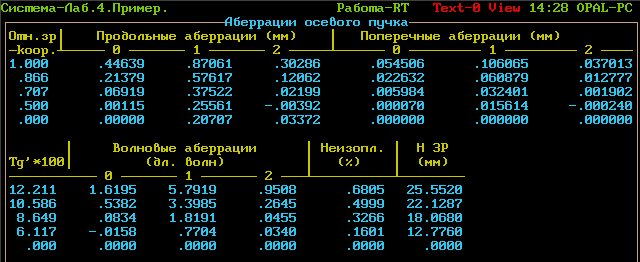
Текстовый режим:

Графический режим:

В изображении осевой точки, если излучение монохроматическое, присутствует только одна аберрация - сферическая. Если в излучении присутствует несколько длин волн, то возникают также хроматизм положения и сферохроматизм.

В данной лабораторной работе необходимо определить величину продольной, поперечной и волновой аберраций осевого пучка, хроматизм и неизопланатизм.

Таблица численных значений аберраций оформляется в виде:

отн. зр. коор.	Продольные аберрации (мм)			хроматизм	Поперечные аберрации (мм)
1.000	0.44639	0.87061	0.30286	0.56775	0.054506	0.106065	0.037013
0.866	0 .21379	0.57617	0.12062	0.45555	0.022632	0.060879	0.012777
0.707	0.06919	0.37617	0.02199	0.35418	0.005984	0.032401	0.001902
0.500	0.00115	0.25561	-0.00392	0.25953	0.000070	0.015614	-0.000240
0.000	0.00000	0.20707	0.03372	0.17335	0.000000	0.000000	0.000000
отн. зр. коор.	Волновые аберрации (дл. волн)			неизопл.	зр. коор.
1.000	1.6195	5.7919	0.9508	0.6805	25.5520
.866	0.5382	3.3985	0.2645	0.4999	22.1287
.707	0.0834	1.8191	0.0455	0.3266	18.0680
.500	-0.0158	0.7704	0.0340	0.1601	12.7760
.000	0.0000	0.0000	0.0000	0.0000	0.0000

Хроматизм на оси - это хроматизм положения, остальные значения хроматизма - сферохроматизм.

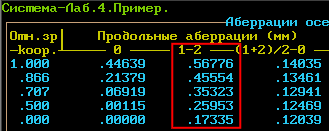
Чтобы сравнить вычисленное значение сферохроматизма с приведенным в OPAL-е, необходимо поменять настройки пункта «Аберрации осевого пучка» как показано на рисунке:

Значения хроматизма положения и сферохроматизма выделены цветом.

4.3.3. Определение диаметра пятна рассеяния

В геометрическом приближении диаметр пятна рассеяния можно определить по максимальной величине поперечной аберрации:

Максимальное (по модулю) значение поперечной аберрации для центральной длины волны , следовательно, диаметр пятна рассеяния:

.

Более точно определить диаметр пятна рассеяния можно в OPAL-е, пункт «Анализ геометрического изображения / Точечная диаграмма». Чтобы исследовать пятно рассеяния для центральной длины волны, нужно установить параметр «Характеристики <Монохроматические>», и чтобы значение было более точным, установить количество точек на зрачке 1152.

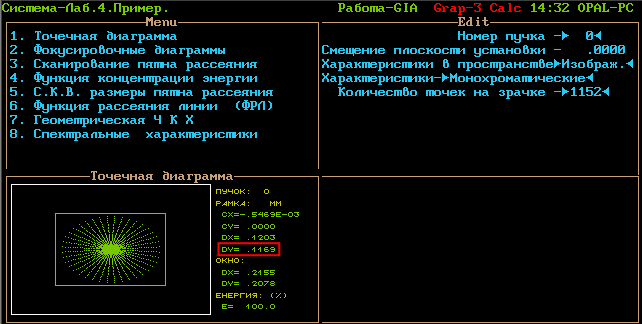
Изменяя размер рамки (клавиши «+» и «- » на дополнительной клавиатуре), необходимо найти минимальный размер рамки, при котором в нее попадают все лучи. В этом случае диаметр рамки (на рисунке выделено цветом) будет соответствовать диаметру пятна рассеяния:

Диаметр пятна рассеяния, в который попадает 80% энергии, также определяется при помощи рамки (по нажатию клавиши «Enter» вычисляется энергия лучей, попавших в рамку).

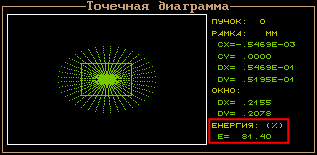
В данном случае, диаметр пятна рассеяния, в который попадает 80% энергии .

4.3.4. Определение плоскости наилучшей установки

Определить плоскость наилучшей установки можно при помощи пункта «Фокусировочные диаграммы». В настройках необходимо задать начальное смещение плоскости установки и шаг по расфокусировке, и подобрать их значения таким образом, чтобы найти положение плоскости установки, в котором диаметр пятна рассеяния будет минимальным, с точностью до 0.05 мм.

Вначале можно задать начальное смещение 0 мм, и шаг по расфокусировке 0.1 мм:

Затем из рисунка можно определить смещение, при котором диаметр пятна рассеяния будет минимальным. Величина смещения относительно начального для каждого кружка рассеяния приведена в верхней части окна. В данном случае минимальное пятно рассеяния будет при смещении 0.2 мм.

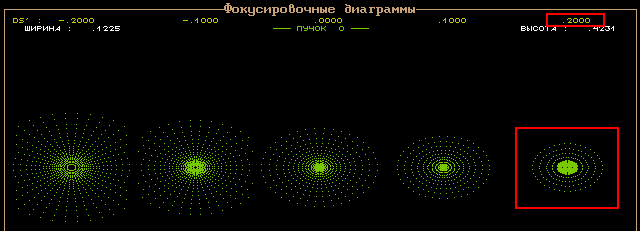
Однако, возможно самое минимальное пятно рассеяния будет при еще большем смещении, поэтому нужно задать найденное смещение (0.2 мм) как начальное и еще раз посмотреть на результат. Таким образом, нужно добиться того, чтобы минимальное пятно рассеяния было не на краю рисунка, а в центре. В данном случае минимальный диметр будет при смещении 0.1 мм относительно начального 0.2 мм, т.е. окончательное смещение 0.1 + 0.2 = 0.3 мм.

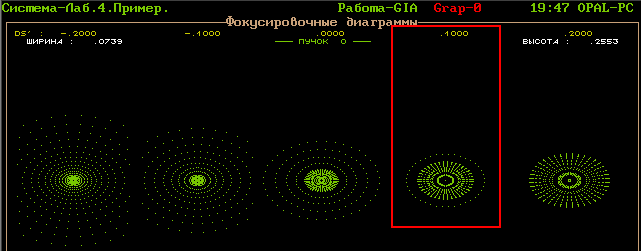
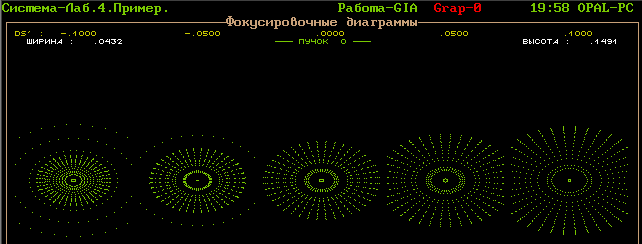
Теперь полученное смещение нужно задать как начальное, уменьшить шаг по расфокусировке до 0.05 мм и найти окончательное смещение.

Таким образом, общее смещение плоскости установки: .

Приблизительно определить плоскость наилучшей установки можно через максимальную величину продольной аберрации: . В данном случае вычисленное значение плоскости наилучшей установки совпадает с подобранным по фокусировочным диаграммам с точностью до 0.03 мм.

4.3.5. Определение диаметра пятна рассеяния в плоскости наилучшей установки

Диаметр пятна рассеяния в плоскости наилучшей установки определяется при помощи точечных диаграмм:

Диаметр пятна рассеяния

Диаметр пятна рассеяния, содержащий 80% энергии .

4.3.6. Определение аберраций осевого пучка в плоскости наилучшей установки

Чтобы определить аберрации осевого пучка в плоскости наилучшей установки, необходимо в пункте «Формирование / Предмет, изображение, диафрагма» задать вычисленное смещение плоскости изображения от плоскости Гаусса:

Текстовые значения и графики поперечных аберраций в плоскости наилучшей установки показаны на рисунке. Из рисунка видно, что поперечные и волновые аберрации стали значительно меньше.