

|
|
|||||


|
|||||
|
| |||||
8.1. Формы представления аберраций
|
|
(8.1.2) |
Зрачковые координаты определяют положение луча в пучке.
Канонические (относительные) зрачковые координаты определяются следующим
образом:
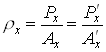 ,
, 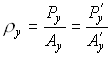 (8.1.3)
(8.1.3)
где ![]() ,
, ![]() – входные и выходные реальные зрачковые координаты,
– входные и выходные реальные зрачковые координаты, ![]() ,
,
![]() – входные
и выходные апертуры. Апертуры
определяют максимальные значения зрачковых координат.
– входные
и выходные апертуры. Апертуры
определяют максимальные значения зрачковых координат.
Таким образом, верхний
луч пучка имеет координаты ![]() ,
нижний луч пучка –
,
нижний луч пучка – ![]() ,
главный луч пучка –
,
главный луч пучка – ![]() ,
сагиттальный луч –
,
сагиттальный луч – ![]() (рис.8.1.4).
(рис.8.1.4).
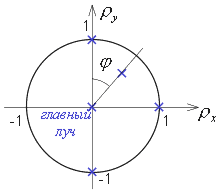
Рис.8.1.4. Канонические зрачковые координаты.
Канонические зрачковые координаты можно выразить через
полярные координаты ![]() и
и ![]() :
:
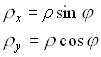 (8.1.4)
(8.1.4)
где ![]() .
.
Волновая аберрация – это отклонение реального волнового фронта от идеального (рис.8.1.5), измеренное вдоль луча в количестве длин волн:
|
(8.1.5) |
Из выражения (8.1.5) следует, что волновая аберрация пропорциональна отклонениям оптических длин лучей пучка. Поэтому влияние волновой аберрации на качество изображения не зависит от типа изображения, а определяется тем, сколько длин волн она составляет.
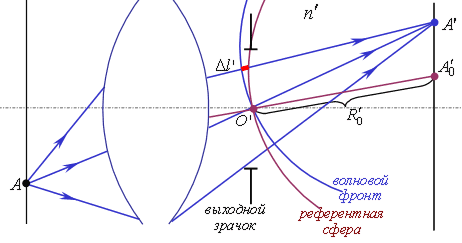
Рис.8.1.5. Волновая аберрация.
Референтная сфера – это волновой фронт идеального
пучка с центром в точке идеального изображения ![]() ,
проходящий через центр выходного зрачка
,
проходящий через центр выходного зрачка ![]() .
При нахождении волновой аберрации с референтной сферой сравнивается ближайший
к ней волновой фронт.
.
При нахождении волновой аберрации с референтной сферой сравнивается ближайший
к ней волновой фронт.
Для всего пучка волновая аберрация – это функция канонических зрачковых координат:
|
(8.1.6) |
Поперечная и волновая аберрации – это разные формы представления одного явления, они связаны между собой соотношениями:
|
(8.1.7) |
Таким образом, поперечные аберрации прямо пропорциональны первым частным производным волновой аберрации по каноническим координатам.
Продольные аберрации –
это отклонения координаты точки ![]() пересечения реального луча с осью от координаты точки
пересечения реального луча с осью от координаты точки ![]() идеального изображения вдоль оси (рис.8.1.6):
идеального изображения вдоль оси (рис.8.1.6):
|
(8.1.8) |
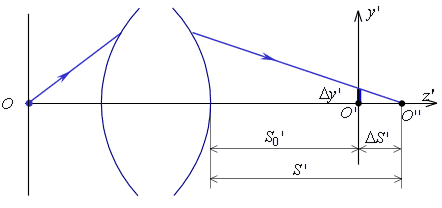
Рис.8.1.6. Продольные аберрации осевого пучка для изображения ближнего
типа.
Для изображения ближнего
типа продольные аберрации выражаются в миллиметрах, для изображения
дальнего типа (рис.8.1.7)
продольные аберрации выражаются в обратных миллиметрах:
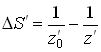 ,
, ![]() (8.1.9)
(8.1.9)
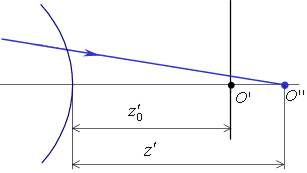
Рис.8.1.7. Продольные аберрации осевого пучка для изображения дальнего
типа.
Продольные аберрации связаны с поперечными, и, следовательно, с волновыми тоже:
|
(8.1.10) |
Выражение (8.1.10) приближенное, оно может использоваться только для случая небольших апертур.
Итак, из выражений (8.1.7) и (8.1.10) следует, что волновая, поперечная и продольная аберрация – это разные формы представления одного явления нарушения гомоцентричности пучков. При оценке качества изображения за исходную модель аберрационных свойств оптической системы берут волновую аберрацию (по величине волновой аберрации судят о качестве оптической системы). Однако, если аберрации велики, то более целесообразно использовать для оценки качества изображения поперечные аберрации.