2.6. Освещенность, создаваемая различными источниками
(закон обратных квадратов)

2.6.1. Освещенность, создаваемая точечным источником

Рассмотрим точечный источник.

Точечный источник – это источник, размерами которого можно пренебречь по сравнению с расстоянием до него, и который излучает поток, равномерный по всем направлениям.

Рис.2.6.1. Освещенность, создаваемая точечным источником.

Освещенность площадки , создаваемая точечным источником:

Освещенность, создаваемая точечным источником обратно пропорциональна расстоянию от источника до поверхности и прямо пропорционально косинусу угла, между направлением светового потока и нормалью к освещаемой поверхности:

(2.6.1)

где – сила света источника в направлении освещаемой точки.

Практические измерения показывают, что для соблюдения закона обратных квадратов отношение размера источника к расстоянию до него должно быть меньше 0.1.

2.6.2. Освещенность от протяженного ламбертовского источника

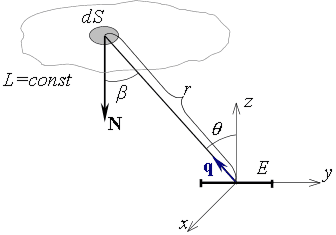
Рис.2.6.2 Освещенность от протяженного ламбертовского источника.

Для протяженного источника можно разбить поверхность источника на элементарные площадки (рис.2.6.2) и определить освещенность, создаваемой каждой из них по закону обратных квадратов:

      (2.6.2)

Проинтегрируем теперь элементарную освещенность по всей площади источника:

      (2.6.3)

Так как у ламбертовского источника яркость постоянна по всем направлениям, ее можно вынести за интеграл:

      (2.6.4)
или

      (2.6.5)

где – орт направления на источник; , – направляющие косинусы.

Можно показать, что выражения (2.6.4) и (2.6.5) эквивалентны, если учесть, что , , , а углы и являются дополнительными к , .