1.4. Регистрируемые (наблюдаемые) характеристики поля

1.4.1. Интенсивность поля

Амплитуда поля не может непосредственно наблюдаться или измеряться, так как поле очень быстро меняется во времени с частотой и , а любые приемники излучения имеют значительно большее, чем период колебаний, время инерции . Поэтому регистрируется лишь усредненная во времени величина – интенсивность поля .

Из уравнений Максвелла следует, что интенсивность пропорциональна квадрату амплитуды поля , то есть равна квадрату модуля комплексной амплитуды (произведению комплексной амплитуды на величину, комплексно сопряженную ей):

(1.4.1)

Можно измерить квадрат модуля комплексной амплитуды, но невозможно измерить фазу и эйконал поля – при регистрации поля они теряются. Для сохранения информации о фазе (эйконале) требуется измерение интенсивности поля, складываемого из нескольких полей.

1.4.2. Наблюдаемые величины при сложении полей

При сложении двух полей (с фазой ) и (с фазой ), суммарную интенсивность можно представить в виде:

Таким образом, суммарная интенсивность записывается в виде уравнения интерферограммы:

(1.4.2)

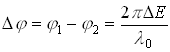где – разность фаз поля.

Явление, возникающее при сложении двух полей, называется интерференцией, а интерферограмма – это картина, наблюдаемая при интерференции.

Сложение когерентных полей

Когерентные поля характеризуются тем, что разность фаз (эйконалов) двух полей остается постоянной за время инерции приемника.

В этом случае суммарная интенсивность определяется выражением (1.4.2), а картина распределения интенсивности представляет собой чередование темных и светлых полос, конфигурация которых зависит от изменения разности фаз .

Введем понятие референтного (эталонного) поля, которое имеет известную картину фаз. При сравнении с ним выявляются параметры другого поля (интенсивность и фаза). Регистрируемая картина взаимодействия двух полей, одно из которых референтное, называется голограммой. Голограмма – это запись полной информации о поле, то есть его комплексной амплитуды. Интерферограмма и голограмма – способы записи комплексной амплитуды поля путем сравнения его с эталонным полем.

Сложение некогерентных полей

Если разность фаз полей меняется случайным образом много раз за время регистрации, то поля являются некогерентными. При регистрации суммарной интенсивности ее значения по времени усредняются:

      (1.4.4)

В выражении (1.4.4) и – постоянны, их можно не усреднять, а , тогда, получим выражение для сложения двух некогерентных полей:

(1.4.5)

1.4.3. Квазимонохроматическое и полихроматическое поле

Поле, излучаемое реальными источниками света, не бывает строго монохроматическим. Оно бывает лишь очень близким к полной монохроматичности, то есть квазимонохроматическим. Полихроматическое поле можно считать суммой (суперпозицией) монохроматических составляющих, а интенсивность такого суммарного поля вычислять следующим образом:

      (1.4.6)
где – распределение интенсивности монохроматической составляющей по длинам волн, – весовая спектральная функция (например спектральная чувствительность приемника), и – реальные границы диапазона излучения.

На рис.1.4.1 показан пример графика распределения интенсивности и весовой спектральной функции.

Рис.1.4.1. Интенсивность и весовая спектральная функция.

1.4.4. Простейшие монохроматические волны

Рассмотрим два типа волн: плоские волны и сферические волны.

Плоские волны

Плоские волны (plane waves) называются так потому, что они имеют плоские волновые фронты (рис.1.4.2).

Рис.1.4.2. Плоские волны.

Волновой фронт – это поверхность в пространстве, на которой эйконал поля (или фаза) имеет одинаковые значения:

(1.4.7)

Различным значениям постоянной соответствуют разные волновые фронты. Если менять , то волновой фронт будет перемещаться в пространстве, переходя из одного состояния в другое. Поле распространяется в сторону увеличения .

Направление распространения света перпендикулярно волновым фронтам, как показано на рис.1.4.2.

Длина вектора, показывающего направление, может быть выбрана различным образом:

• – единичный вектор направления (орт), ;
• – волновой вектор, , где – волновое число;
• – оптический лучевой вектор, ,
        (1.4.8)

Все эти векторы (, , ) имеют одинаковое направление (в сторону распространения поля), но разную длину.

Уравнение плоской волны имеет следующий вид:

(1.4.9)

Для плоской волны амплитуда постоянна, меняется только эйконал, который можно записать как уравнение плоскости:

(1.4.10)

Из аналитической геометрии следует, что при таком описании эйконала волновой фронт плоский и перпендикулярен вектору распространения, то есть оптическому лучевому вектору . Плоские волны замечательны тем, что любое сложное поле можно представить в виде совокупности плоских волн. Поэтому эти волны являются универсальным базисом для описания световых полей.

Сферические волны

Сферические волны (spherical waves) имеют волновой фронт в виде концентрических сфер (рис.1.4.3).

Рис.1.4.3. Сферические волны.

Поместим систему координат в центр, тогда получим следующие выражения для комплексной амплитуды и эйконала сферической волны.

Уравнение сферической волны:

(1.4.11)

Уравнение эйконала сферической волны:

(1.4.12)

где – это длина радиус-вектора точки в пространстве.

Сферические волны так же, как и плоские, могут быть использованы для представления сложных полей, кроме того, плоские волны можно считать частным случаем сферической волны с бесконечно малой кривизной волнового фронта.